Unjamming Traffic

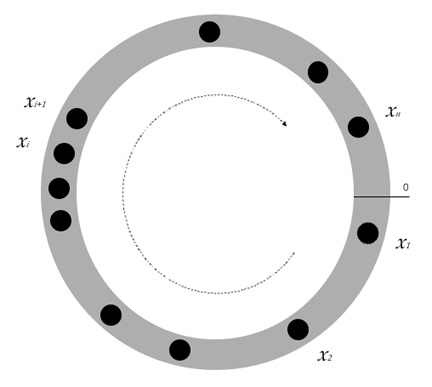
Figure 1: Cars are represented by the black dots and travel clockwise around the track. The ith vehicle follows the (i+1)th vehicle and the nth car follows the 1st.

Traffic jams often occur for seemingly no reason, especially when you are going somewhere in a hurry. It is a common occurrence on busy roads to be brought to a stand-still when there is no ostensible cause for the delay. Mathematicians from the Universities of Exeter, Bristol and Budapest have developed a model of traffic behaviour that explains how an unexpected event as simple as a car changing lanes, or a van braking suddenly, can bring traffic to a grinding halt kilometres behind the incident. They have recently published their work in Proceedings of the Royal Society.

Their model suggests that when reacting to an unexpected event, drivers may slow down to below a critical speed, which then forces the car behind it to slow down further still. Eventually, cars further back in the queue must stop. This produces a wave travelling backwards from the point of disturbance.

The modelling is based on bifurcation theory, which studies how and when mathematical problems change from having only one possible solution to having many. Parameter values at which this change occurs are known as bifurcation points. In the traffic example, the important parameter is the average headway between cars on the road: if this value is large, then small incidents do not cause the system to change significantly. However, if it is too small, the cars do not have enough time to react to an incident and a stop-and-go wave can develop throughout the traffic.

The model uses a circular road of length L, around which n cars travel. The group suggests that this could be interpreted as traffic on a circular road around a large city such as the M25 around London. The cars and drivers are assumed to be identical, the ith vehicle follows the (i+1)th vehicle and the nth car follows the 1st. This can be seen in Figure 1. The model uses a differential equation that relates the motion of the cars to the headway: \ $$ \ddot{x}_i(t) = \alpha (V(h_{i}(t-1)) - \dot{x}_i(t)); $$ where\ $ x_i $ is the position of car\ $ i, $ \ $ L $ is the length of the track,\ $ \dot{x} $ and\ $ \ddot{x} $ are the time derivatives of\ $ x $ — velocity and acceleration — and\ $ \alpha $ is a known sensitivity factor. \ $ L $ is the known optimal velocity function and depends on the headway between car\ $ i $ and the one in front:\ $ h_{i} = x_{i+1} - x_{i} $ . As the cars are travelling in a circle, \ $ h_n = x_1 - x_n $ .

The team considered solutions for car position and velocity with regard to the headway parameter, and identified parameter values at which bifurcations occurred. Some variation in traffic speed can be absorbed by the system to maintain smooth traffic flow, however if the average headway is too small, the system no longer has the single steady flow solution in which the velocity of the cars remains smooth and above zero, but two solutions: a steady flow solution and one in which the traffic is stop-start and vehicle velocities periodically drop to zero. This second solution produces a stop-and-go wave. Such a backward travelling wave can die out by itself, or get worse, ending up as a persistent stop-and-go wave that travels around the whole circle.

The group predicts this behaviour on busy highways with more than 15 cars per kilometre. Heavy traffic does not automatically lead to congestion, but the model suggests, as every driving instructor teaches, that drivers should give themselves enough headway to react to an unforeseen event so that they do not have to slow down too suddenly. The authors suggest that overhead gantries on freeways could display temporary and variable speed limits that, if followed by the traffic, would overcome jams and return the traffic to uniform flow. The MIDAS system installed on the M25 motorway around London is currently able to provide this information to drivers. The team now plans to expand on the model and incorporate cars fitted with new electronic devices that increase reaction time and so cut down on over-braking.