A very useful pandemic

It may just be a matter of time before the next influenza pandemic strikes. Stephen Kissler, from the Cambridge Infectious Diseases group in DAMTP, is part of a group of Cambridge mathematicians who have just worked with the BBC on a programme, Contagion! The BBC Four Pandemic, and together they have run a ground-breaking citizen science experiment that will help fight future pandemics.

There were two parallel aims for the project. One was producing the documentary with the BBC, describing the science and mathematics behind epidemiology, and the work that is being done on modelling and preparing for influenza epidemics and pandemics. "The second objective was more scientific," says Kissler. "This was to conduct a massive citizen science experiment which collected (with permission) data on people's movement, their reported contacts, and some personal information."

People participated (and can continue to participate, see below) by downloading the BBC Pandemic app on their smartphone (via the App Store or Google Play). The app asked for their age and gender, and then recorded their location every hour for 24 hours. At the end of that period the participant then recorded how many people they had contact with over that period, and some details about the interactions (eg. conversational versus physical contact, age of contact).

The result has been a "state of the art data set which will change how we develop infectious disease models," says Kissler. The original aim of the project was for around 10,000 people to participate. The project far surpassed that aim with nearly 30,000 people around the UK took part, making it the biggest citizen science experiment of its type, and the biggest such data set ever created. "There are no datasets on interpersonal contact that are that big," says Kissler. "The really crucial thing is this data links reported contacts with movement data, with how these people moved about in space. This has never been done before."

Modelling gravity

One of the models used by epidemiologists like Kissler is called a gravity model, named because of its similarity to Isaac Newton's law of gravitation. Newton's law says that the gravitational attraction between two bodies (of masses $m_1$ and $m_2$) is proportional to $$\frac{m_1{m}_2}{d^2}$$ where $d$ is the distance between them. Researchers believe a similar rule is true for how people move between two locations.

"A gravity model describes how the frequency of human movement decays with distance, just like the force of gravity decays with distance," says Kissler. This model of movement then forms part of a model of how a disease is spread, as the infection passes from person to person. In particular, it is used to estimate the likelihood that one city or region will become infected at a certain time, depending on the infectious status of the neighbouring cities and regions, their sizes and distance away.

"The new data means we can test this model for its accuracy for predicting how people will move," says Kissler. The data will give them more accurate parameters for the model, in particular the power to which you raise the distance (the power of $d$ is 2 in Newton's law). And because of the fantastic detail available in the new dataset, the researchers can see how this varies for different ages.

For the first time they now have detailed insight into the differences in movement patterns between age groups – a key thing they are interested in as epidemiologists. "A certain amount is known about how adults move around, how they commute to work and so on," says Kissler. "But we have no idea how people under 20 move around. And this is very important to the spread of lots of diseases, such as influenza, which is believed to be spread, particularly, by school-age children." The new data will allow researchers to test this theory of school-age children spreading influenza and see whether it is accurate.

Planning for the future

Although the simulations for the programme were bleak (predicting 43 million people infected in the UK, and nearly 900,000 dead, before a vaccine could realistically be produced), Kissler emphasises these simulations weren't a robust prediction of the potential impact of a pandemic: "We do this quantitative analysis, but we are interested in [using these] to compare qualitative outcomes."

In particularly, these simulations allow researchers to assess the impact of interventions on the spread of a disease. A simulation in the programme showed how a pandemic could be drastically slowed down by everyone in the country rigorously washing their hands.

Such interventions are introduced into the models by changing the value of the reproductive ratio, $R_0$ , which is the average number of people an infected person will pass the disease onto. (You can read more in The mathematics of diseases.) "For a disease to spread $R_0$ needs to be greater than 1," says Kissler. In their first simulation of the pandemic for the programme, where nearly 900,000 died, $R_0$ was set to 1.8. In the hand-washing scenario, $R_0$ was only slightly lower, at 1.5, but reduced the number of cases and deaths of the disease by a quarter.

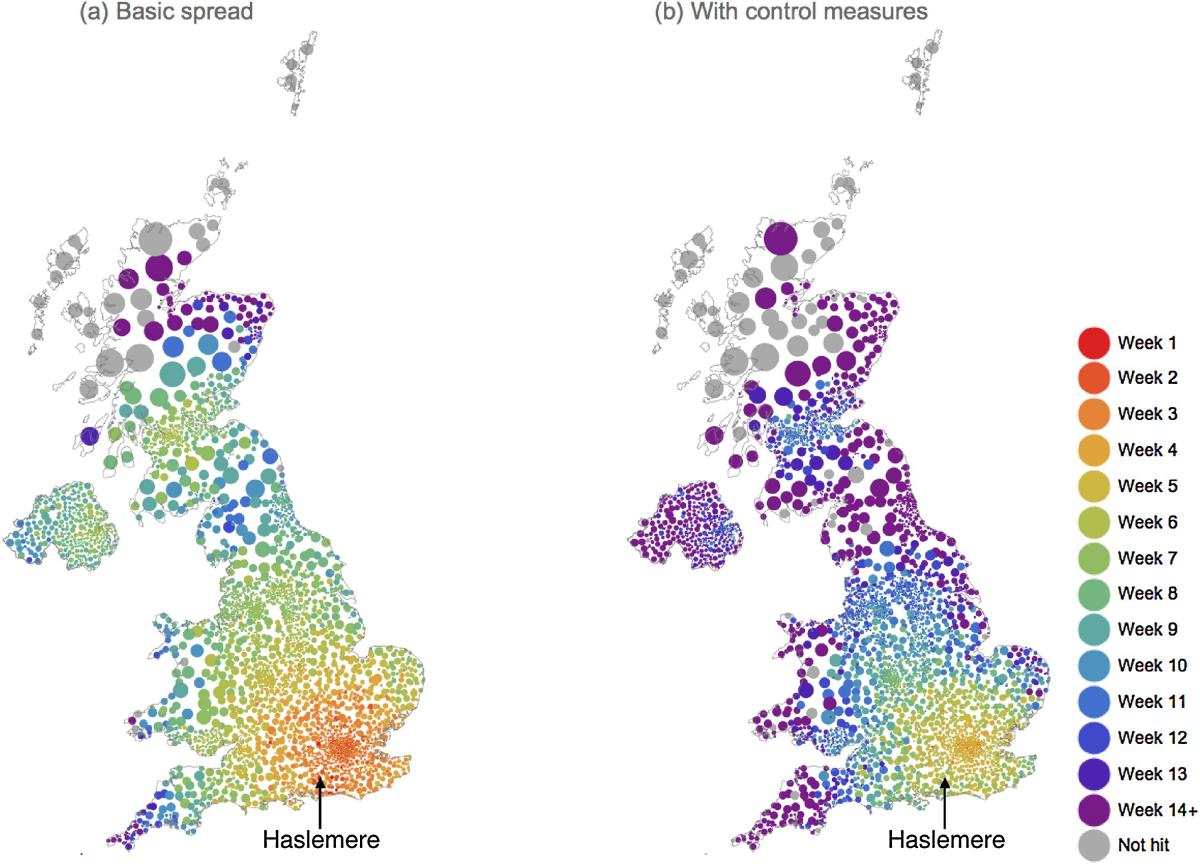
The geographic spread of the disease for the uncontrolled pandemic on the left. (Note that the area of the disks are related to the geographic area of the regions in the model, not the population density.) The map on the right shows the spread of the disease when extra hand washing is introduced. (Image from paper by Klepac, Kissler and Gog, CC BY-NC-ND 4.0)

The team, Professor Julia Gog, Dr Petra Klepac and Kissler, are now busy completing their initial data analysis, which they will publish along with the whole data set in early 2019. Then, as well as continuing with their own research, they are looking forward to seeing what the rest of the scientific community, including those outside of epidemiology, do with the data set.

Mathematical models of pandemic disease play an important role in policy decisions and government planning for future pandemics. "The clearest example is the foot and mouth outbreak in the UK," says Kissler. "Several modelling teams tested interventions using different models," agreeing on the best interventions to implement. "This data set will hopefully make that link between [mathematics and public policy] stronger."

You can also still contribute to this dataset by downloading the app and becoming part of this groundbreaking citizen science experiment. The researchers are particularly interested in more teenagers and people over the age of 60 taking part. And you can run the app more than once, contributing data on say, a week day, and then on a weekend, which would give researchers information on how our movement patterns change.

And in case you are still worried about a future pandemic, what can we as individuals do to prepare? Kissler has some practical advice: wash your hands, and cover you mouth when you sneeze!

You can read more about the mathematics behind the programme in the researchers' paper: Contagion! The BBC Four Pandemic – The model behind the documentary. And you can read more about the maths of pandemics in our coverage of the COVID-19 pandemic. (This article was updated Nov 2021.)