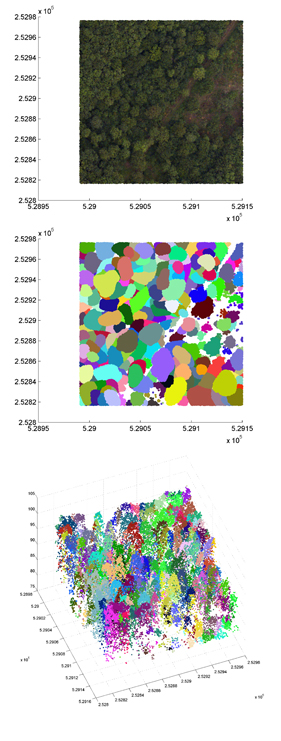
Top image: An area of English forest. Centre image: Individual trees have been isolated. Bottom image: A 3D version of the isolated tree image. (All images: Juheon Lee)

Pictures play a vital role in our lives. They allow us to discover the world, to understand it and to enjoy it. Our own pair of eyes is a powerful tool, but modern imaging technology goes a lot further, revealing distant galaxies and tiny cells in our bodies. Mathematics is the language that underlies this technology, which is why the Cambridge Image Analysis Group, led by Carola-Bibiane Schönlieb, is at home in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge.

The Cambridge Image Analysis Group produces techniques that can be used in a wide range of areas, from renovating artwork to restoring satellite images. A recent example is a method that finds application in two very different contexts: forest ecology and the treatment of cancer patients. It's the result of collaborations with the Forest Ecology and Conservation Group at the Department of Plant Sciences, the Department of Engineering, the Cavendish Laboratory and Addenbrooke's Hospital.

Forest ecologists and medical scientists face a similar problem: to recognise objects in an image automatically. For the medical scientist the objects may be healthy organs in a patient's body that need to be protected from harmful radiation during treatment of cancerous organs. Since an organ might be in a slightly different position at every therapy session, the aim is to create a technique that automatically pin-points its location and then applies the radiation accordingly.

For the forest ecologist the objects are trees. Scientists need to take stock of the number and types of trees in areas so large that individual counting is unfeasible. Instead, they take different types of images from the air: ordinary photographs; hyperspectral images, which also give information about the material make-up of the trees; and Lidar data, which record information on their height. Ideally a computer would analyse these images and come up with a final tally of trees.

Mathematics can help because, when stored in a computer, a picture is essentially a list of numbers: each pixel is defined by its location (given by two co-ordinates) and its colour (given by a numerical value) and perhaps some additional numerical information that has been recorded for that pixel. When there is more than one image of the same scene, as is the case with the forests, then the first task is to overlay them correctly: to find a map that relates a pixel in one image to the corresponding pixel in another. Since the images look quite different this can be a difficult problem. How do you know which pixel corresponds to which? Mathematicians have solved this conundrum by turning it into a minimisation problem. First they define a mathematical object that measures the difference between two images. Then, out of all the possible maps between the two images, they find the one that minimises that difference.

The next task, both for the trees and also for medical imaging, is to pick out the contours that separate one object (say, a tree or an organ) from its surroundings. Again this can be solved using minimisation. Put simply, you look for contours that separate the picture into different regions so that the average numerical value of pixels within any one region equals a prescribed value, which is also found using minimisation.

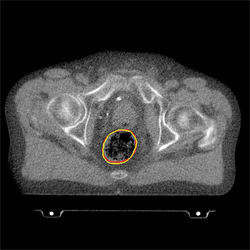
The position of a patient’s rectum has been pin-pointed (Image: Dr Xiaohao Cai)

Problems that call for the minimisation (or maximisation) of quantities subject to constraints are called variational problems. They have a long history in mathematics and are often fiendishly difficult to solve. Not only can it be difficult to define the object that is to be minimised or maximised (how do you define the difference between two images?), but additional constraints are often needed to find a unique solution. When searching for the outline of objects, for example, many contours might present themselves as candidates and you need a way of picking the "best". This depends on the context: for example, you might decide to go with the ones of shortest length. Variational problems are usually phrased in the language of partial differential equations, which can be used to describe how one quantity changes as another is varied.

The work of the Image Analysis Group has resulted in a software tool (in collaboration with the Cancer Research UK VoxTox Research Group, Cambridge) that is currently being tested at the Cavendish Laboratory here in Cambridge. The tree counting method is being validated on data from around the world. The Image Analysis Group's work crosses the borders between a host of different disciplines. It is part of the IMAGES network, which brings together leading academics from all six Schools of the University of Cambridge, international experts and research-led industries to work on pioneering imaging technologies.

About this article

Carola-Bibiane Schönlieb is head of the Cambridge Image Analysis Group at the Department of Applied Mathematics and Theoretical Physics, University of Cambridge.

You can download this article as a poster for display in classrooms, at science festivals, or wherever else you'd like to see it. You can also watch Carola talk about her work in this short video.