When things get weird with infinite sums

Luciano Rila
Submitted by Marianne on December 18, 2014

Things can get weird when we deal with infinity. Consider the following sum

  \[ S = 1-1+1-1+1-1+1-1+ ... \]    

It’s called Grandi’s series, after Italian mathematician, philosopher, and priest Guido Grandi (1671-1742).

If we group its terms this way

  \[ S = (1-1) + (1-1) + (1-1) + (1-1) + ... \]    

it’s easy to see that $S$ should be equal to $0$ because each individual bracket is equal to $0.$ Nothing stops us, however, from grouping its terms in a different way, for example

  \[ S = 1 + (-1+1) + (-1+1) + (-1+1) + ..., \]    

in which case $S$ should be equal to $1$! There is even a third way of evaluating this sum. Say that we rewrite it as

  \[ S = 0+1-1+1-1+1-1+... \]    
Grandi

Guido Grandi (1671-1742).


All we did was to add a zero at the start so I hope we can agree that we haven’t changed the sum at all. If we now write $S$ twice

  \[ S = 1-1+1-1+1-1+1-1+ ... \]    
  \[ S = 0+1-1+1-1+1-1+1- ... \]    

and add them together we get

  \[ S+S = 2S = (1+0)+(-1+1)+(1-1)+(-1+1)+... \]    

Hence $2S$ should be equal to $1,$ which gives that $S$ should be equal to $\frac{1}{2}.$

Infinite but tame

As you can see, sums containing an infinite number of terms, known as infinite series, can challenge our understanding of very basic mathematical concepts such as addition and subtraction. Our next stop in our exploration of infinite series is the following geometric series:

  \[ S = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ... \]    

There's a clever way of figuring out the value of this sum, using the diagram below

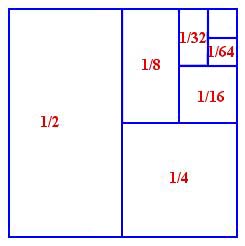
diagram

Take a square of side length $1$ and it divide it in half to get two rectangles, which both have area $\frac{1}{2}.$ Now divide one of those rectangles in half as shown, to get two squares of area $\frac{1}{4}.$ Divide one of those squares in half to get two rectangles of area $\frac{1}{8},$ and so on, ad infinitum. The total area (of the squares and rectangles we left undivided) is the same as the sum of all terms of the geometric series. Since that area is just the area of the large square, the geometric series appears to be equal to $1.$

And indeed, mathematicians agree with this statement. They say that the series converges to $1.$ Formally convergence is defined by looking at the sequence of partial sums:

  $\displaystyle S_1 $ $\displaystyle = $ $\displaystyle \frac{1}{2} $    
  $\displaystyle S_2 $ $\displaystyle = $ $\displaystyle \frac{1}{2} + \frac{1}{4} = \frac{3}{4} $    
  $\displaystyle S_3 $ $\displaystyle = $ $\displaystyle \frac{1}{2} + \frac{1}{4} + \frac{1}{8} = \frac{7}{8} $    
  $\displaystyle S_4 $ $\displaystyle = $ $\displaystyle \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} = \frac{15}{16} $    

and so on.

The partial sums gives us a sequence of numbers, $\frac{1}{2}, \frac{3}{4}, \frac{7}{8}, \frac{15}{16}, ...$ which get closer and closer to $1;$ in fact they get arbitrarily close to $1$ as we include more and more terms. In general, when the sequence of partial sums of an infinite series converges on some limit number $a$ in this way, then we say that the infinite series converges to $a.$

Notice that this doesn’t happen for the Grandi’s series above. The partial sums are

  $\displaystyle S_1 $ $\displaystyle = $ $\displaystyle 1 $    
  $\displaystyle S_2 $ $\displaystyle = $ $\displaystyle 1-1=0 $    
  $\displaystyle S_3 $ $\displaystyle = $ $\displaystyle 1-1+1=1 $    
  $\displaystyle S_4 $ $\displaystyle = $ $\displaystyle 1-1+1-1=0 $    

and so on. The partial sums eternally skip from 1 to 0 and back again. They don’t converge to a limiting value, so there’s no obvious way of assigning a value to the series.

Infinite and divergent

It seems fairly intuitive that the geometric series above should converge to 1. The individual terms of the series, $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}$ and so on get smaller and smaller. So although we are constantly adding things to make the sum bigger and bigger, the amount we are adding eventually becomes so small, it’s no surprise we never exceed 1. This argument however is flawed. Let’s take a look at the harmonic series:

  \[ S = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... \]    

Similarly to the geometric series we investigated above, the terms of the harmonic series get smaller and smaller. But surprisingly the harmonic series diverges: the terms in the sequence of partial sums get bigger and bigger, eventually exceeding all bounds. We say that the series tends to infinity.

The harmonic series diverges

The harmonic series diverges


If this sounds hard to believe, here is a proof by contradiction of the divergence of the harmonic series. In a proof by contradiction we start by assuming that the opposite of what we are trying to prove is true and then show that this leads to a contradiction. If we are trying to prove statement $A$ is true, then we start by assuming the opposite: that not $A$ is true. If this assumption leads to a contradiction, then this implies that the not $A$ must be false, so our original statement $A$ must be true. In this case, we want to show that the harmonic series diverges, so we assume that the harmonic series converges to some positive value $H.$

We know that

  \[ \frac{1}{3}>\frac{1}{4}, \]    
  \[ \frac{1}{5}>\frac{1}{6}, \]    
  \[ \frac{1}{7}>\frac{1}{8}, \]    

and so on. So if we replace the fractions with odd denominators by their consecutive even ones we find the following inequality

  \[ H = 1+\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6}+\frac{1}{7} +\frac{1}{8}+ ... > 1+\frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{6} + \frac{1}{6}+\frac{1}{8} +\frac{1}{8}+ ... \]    

If we now combine the fractions with the same denominator we get

  \[ H = 1+\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6}+\frac{1}{7} +\frac{1}{8}+ ... > 1+\frac{1}{2}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+... \]    

On the right-hand side the harmonic series appears again, plus an extra term of $\frac{1}{2}.$ This proves that

  \[ H > H+\frac{1}{2}! \]    

As this contradiction followed from our assumption that the harmonic series converges, we can conclude that this assumption is false: the harmonic series does not converge. As the partial sums get larger and larger by smaller and smaller increments (we add a term of the form $\frac{1}{n}$ at every step) the only other possibility is that the sequence of partial sums grows beyond all bounds (rather than skipping around akin to Grandi’s series). This proves that $H$ diverges.

Infinite and bizarre

Things get seriously bizarre when we examine the alternating harmonic series. Built from the harmonic series but with every other term negative, the alternating harmonic series is defined as follows:

  \[ S = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... \]    
Riemann

The mathematician Bernard Riemann (1826-1866) proved an important result about rearrangements of infinite series.

It’s possible to show that the alternating harmonic series converges to $\ln {2} \approx 0.7$ (here $\ln {2}$ stands for the natural logarithm of $2$). You can verify this using a calculator or, if you’re advanced in your calculus, using the Taylor series of $\ln {(x+1)}$ evaluated at $x=1.$

So let’s start with this fact, writing

  \[ \ln {2} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... \]    

Now let’s multiply through by $2$

  \[ 2\ln {2} = 2 - \frac{2}{2} + \frac{2}{3} - \frac{2}{4} + \frac{2}{5} - \frac{2}{6}+\frac{2}{7} - \frac{2}{8}... \]    

If we now simplify the fractions so that all fractions with the even denominators are reduced and then combine the terms with the same denominator – and you can see that only fractions with odd denominators will be combined – we get

  \begin{equation} 2\ln {2} = (2 - 1) - \frac{1}{2} + \left( \frac{2}{3} - \frac{1}{3} \right) - \frac{1}{4} + \left(\frac{2}{5} - \frac{1}{5}\right) - \frac{1}{6} ... \end{equation}   (1)

Removing the brackets we have

  \[ 2\ln {2} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... \]    

The right-hand side is the alternating harmonic series, so we seem to have proved that

  \[ 2\ln {2} =\ln {2} \]    

But, hang on, what? There must be a mistake in our working. I find it hard to believe, but in fact there is nothing wrong with our working. The paradox is explained by the fact that, when we rearrange the terms of the alternating harmonic series, the series converges to a different value. The right-hand side of expression (1) above can be written as

  \[ 2\ln {2} = (2 - 1) - \frac{1}{2} + \left( \frac{2}{3} - \frac{1}{3} \right) - \frac{1}{4} + \left(\frac{2}{5} - \frac{1}{5}\right) - \frac{1}{6} ... = 2\left(1 - \frac{1}{2} - \frac{1}{4} + \frac{1}{3} - \frac{1}{6} - \frac{1}{8} + \frac{1}{5} ... \right). \]    

The problem comes from the fact that while

  \[ 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - ... \]    

converges to $\ln {2},$ the rearranged series

  \[ 1 - \frac{1}{2} - \frac{1}{4} + \frac{1}{3} - \frac{1}{6} - \frac{1}{8} + \frac{1}{5} ... \]    

converges to

  \[ \ln {2}+\frac{1}{2}\ln {\left(\frac{1}{2}\right)}, \]    

despite the fact the two series have exactly the same terms!

Let’s see if we can make sense of this. In the classic formulation of the alternating harmonic series we start with $1$ and subtract $\frac{1}{2}$, then add $\frac{1}{3}$ and subtract $\frac{1}{4}$ and so on. For each added term we subtract exactly one term. In the second formulation of the alternating harmonic series, we subtract two terms for each term that we add. What do you think will happen?

The graph below shows what happens to the partial sums as we add terms one at a time. It shows the first 25 partial sums. The green dots are the partial sums for the classic alternating harmonic series and the purple dots are the partial sums for our rearrangement of the series. The graph shows that the two series will converge to different values.

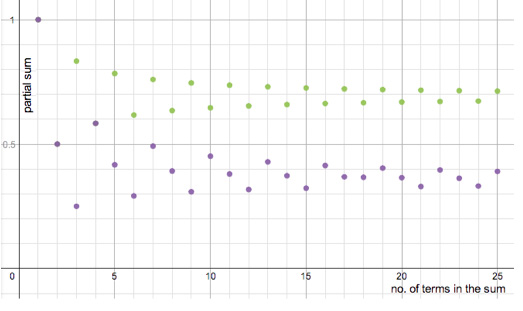
Umbrella

It turns out that by rearranging the alternating harmonic series we can make it converge to any value we like. Try to work out for yourself what value

  \[ S = 1 + \frac{1}{3} - \frac{1}{2}+ \frac{1}{5}+ \frac{1}{7} - \frac{1}{4}+ \frac{1}{9}+ \frac{1}{11}-\frac{1}{6}+ ... \]    

converges to. See here for an answer.

You will be glad to know that, for a series with only positive terms, altering the order of the terms does not affect the sum.

To read more about infinite series see An infinite series of surprises.

About the author

Lucinao Rila

Luciano Rila works in the Department of Mathematics at University College London and is also an Area Coordinator for the Further Maths Support Programme. He is keen to promote the beauty of mathematics to young mathematicians and the general public. He also teaches static trapeze. You can follow him on Twitter @DrTrapezio


Comments

Submitted by Anonymous on December 31, 2014

Please explain to me how I'm missing the big picture, Luciano, but all I can see right now are pieces of logical legerdemain in most accounts of the Grandi series.

Take your pair of examples:

(1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + . . .

1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + . . .

I can't help noticing there are eight 1's in the first, but only seven in the second. So it's not just a matter of "grouping them differently". Adding and subtracting the 1's in accordance with the signs and brackets gives 0 and 1 respectively, but then it's hardly surprising that changing the task results in a different solution. To be consistent the second should be:

1) + (-1 +1) + (-1 + 1) + (-1 + 1) + (-1 + . . .

which does sum to 0.

Similarly with your other example in which you claim all you're doing is adding a zero at the start. I just can't "agree that we haven't changed the sum at all", because once again the quantity of 1's gets simultaneously but silently reduced from eight to seven. In other words, a 1 was sneaked away from the second, or if you like, smuggled into the first series. To be consistent the second should go:

0 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 . . .

Restoring that last "- 1" brings the sum back to 0.

I'm not trying to pour cold water on the fun and fruitfulness of manipulating the various items in the Grandi series. Elsewhere in Plus.Maths I offer it as a model for variable stars.

Submitted by Anonymous on January 7, 2016

It is true that the number of ones shown(!) changes from 8 to seven, but the "..." at the end means that the sum goes on to infinity, i.e. there are infinity "1"s and infinity "-1"s, regardless of how many are written down. You can continue adding in "1"s and "-1"s by hand if you want, but your arm will get tired before infinity, so best to use the "..."!

The point here is that if you pair the terms "1" and "-1" in different parts of the sum, you seem to get a different answer, which is only true because the sum goes to infinity. Going to infinity means that you can just keep adding paired terms that equal 0 in this way, so there seems to be a problem with infinity and making the sum make sense. It is certainly true that for any finite sum there is absolutely no problem with how we group the terms, the answer is the same no matter what. Hope this helps.

Submitted by Naman on August 28, 2016

Well there is another to do it like take the partial sum

like first add 1st term then take average then add 1st and 2nd term then take average and so on then you will notice that your will be 1/2 , 0 , 1/2 , 0 , 1/2 .......

Submitted by Leslie.Green on September 9, 2018

So if you take an alternating series and miss out lots of terms then the partial sum is wrong. How is that bizarre or even interesting? By rearranging the terms and 'forgetting' a few in the new "partial sum" you have made a mathematical error. Obviously if you just rearranged ALL the terms (up to the Nth in the original series) the partial sum result would be the same.

Imagine you put all the positive terms first, letting the negative ones fall off the end because you were only looking at a partial sum. That would not be a mathematically sound approach. What you have shown is something approaching that scheme, but not quite as bad. I imagine that what you have presented is "orthodox" maths. Nevetheless it is a work of sleight of hand, and not sensible. Just because it is an infinite series does not allow one to go crazy!

Submitted by Leslie.Green on September 10, 2018

As I thought, this is text book material. Whittaker & Watson: A Course of Modern Analysis, 4th ed. Chapter 2 example 6 has the sum for (1/2)log 2 which looks as if it is an exam question from 1908. And section 2.4 cites a reference to Dirichlet in 1837.

At each step in the sequence generation, one positive and two negative terms are created. Every partial sum has twice as many negative as positive terms. The claim is that none are omitted since the series is infinite, and yet at any partial sum step 1/3rd of the elements from the original series have been lost.

Infinity doesn't correct the problem as at every subsequent step the problem gets worse! An infinite number of terms does not mean ALL terms.

Submitted by Leslie.Green on June 19, 2019

Every partial sum in the "rearranged" series has missing terms. If these terms sum to a non-zero value then the value of the series has been changed. You CAN do this with the Riemann Zeta function because it is absolutely convergent (for real arguments greater than 1) and the sum of the discarded series is zero.

http://lesliegreen.byethost3.com/articles/rearrange.pdf