
If you can't bend it, model it!
Ball games have universal appeal because of their basic simplicity. For many years (and for many people still), the pleasure lay in simply kicking a ball as fast as possible or striking it sweetly with a bat, racket or club. But as games became more competitive, players began to realise that the ball's flight could be modified to tactical advantage by hitting or kicking it in a particular way. This might involve hooking the ball around an obstacle in golf or swerving it over the defensive wall (a line of footballers standing so as to block a direct shot in a free kick) in a football match.

P G Tait (1831 - 1901)
Exactly when these aerodynamic subtleties began to be exploited in sport is not known with certainty. Isaac Newton was the first scientist to record that a tennis ball would swerve when it was struck with an oblique racket — what we would nowadays call a sliced shot. So far as we know Newton never played tennis but he seized on this example in trying to explain optical refraction, the bending of a ray of light when it passes through a prism.
In his model, light consisted of microscopically small particles — tennis balls in miniature. Presumably the inclined prism face would act just like a racket and deflect the particles accordingly. Newton was wrong on this occasion and very little mathematical insight was applied to the science of ball flight until the mid-19th century when a Scottish mathematician, Peter Guthrie Tait, turned his attention to golf, his favourite game.
Spin's the thing
Tait, Professor of Natural Philosophy at the University of Edinburgh, was intrigued by the relatively long time a ball would remain in the air following a good drive — over six seconds with the equipment of the day. (We tend to laugh at the efforts of golfers of that era as today's big hitters with their high-tech clubs can easily achieve drives over 360 yards, more than twice as far as Tait's professional contemporaries.) Primitive the equipment may have been, but Tait had identified a real issue, one that goes to the very heart of understanding why a ball can be made to do such remarkable things in a swerving free kick.
By modelling a golf ball's flight using the familiar forces of gravity and air resistance, Tait produced a range and time-of-flight that were much too short. But his great insight was to realise that a spinning ball would generate aerodynamic lift, which would prolong the flight considerably. A golf club with its sloping face is almost an exact analogue of Newton's oblique racket, so when it strikes the ball, savage backspin is produced. This results in a vertical force which, depending on spin rate and forward speed, can equal or even exceed the weight of the ball, and for much of its flight a golf ball is effectively weightless.
This third force, only present when the ball is both spinning and moving forwards, is nowadays called the Magnus force after its discoverer, the German physicist Heinrich Magnus who studied air flowing over rotating cylinders. The really interesting thing about the Magnus force is its direction: it is always at right angles to the plane containing the velocity vector and the spin axis. So for a ball spinning about a horizontal axis (that is, pure backspin) the force will be vertical, just as Tait had envisaged. But tilt the spin axis and the deflecting force follows suit. So controlling the inclination of the spin axis, and hence the direction of the Magnus force, is the key to modifying the flight of the ball. This is exactly what happened in the 1950s when a generation of gifted Brazilian footballers invented the swerving free kick. Their method involved striking the ball on its side to give it pure sidespin, producing a horizontal deflecting force.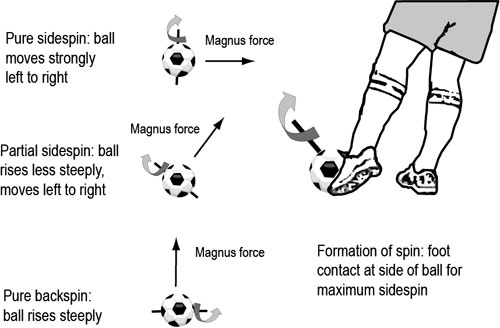
The technique behind a swerving free kick: The direction of the Magnus force is
perpendicular to the direction the ball is moving in (in this diagram it is being
kicked straight through the screen) and the axis around which it is spinning. The
pure sidespin in the top-left figure creates a strong horizontal force, producing the
swerving free kick invented by the Brazilian footballers. Whereas the pure backspin
in the bottom-left figure produces the vertical lift Tait predicted for a golf ball.
The aerodynamics explained
It may seem to be a bold step from golf to football and the kind of swerving free kicks that David Beckham produces, but the aerodynamic principles are exactly the same. The diagram below shows the forces acting on a spinning football: the Magnus force and the drag force, which opposes the ball's motion through the air. Both the drag and Magnus forces follow a v-squared
relationship, and take the general form:
\begin{equation} F= 1/2 \rho A v^2 C \end{equation} Here $\rho$ is the density of air, $A$ the cross-sectional area of the ball and $v$ its speed. $C$ is a dimensionless number that scales the strength of the drag force or Magnus force at a particular speed and it's usual to subscript these coefficients as $C_d$ or $C_m$ to make clear exactly which force is under discussion.
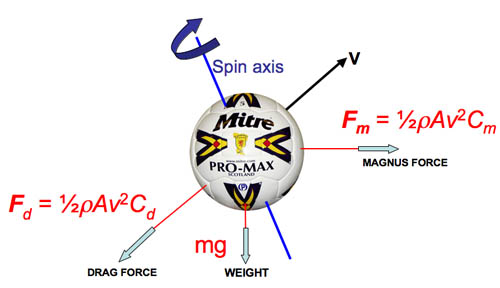
Forces on a spinning ball
Deriving the equation of motion for the ball is not difficult, although care must be taken to assign the directions of the drag and Magnus forces correctly. This is done by defining unit vectors in the direction of the spin axis and the velocity. For a ball spinning about a vertical axis (the z-axis) and moving in the positive x-direction we find: $$ \frac{d^2x}{dt^2}=-vk(C_d\frac{dx}{dt}+C_m\frac{dy}{dt}) $$ \setcounter{equation}{1} \begin{equation} \frac{d^2y}{dt^2}=-vk(C_d\frac{dy}{dt}-C_m\frac{dx}{dt}) \end{equation} $$ \frac{d^2z}{dt^2}=-g-vkC_d\frac{dz}{dt} $$ Here, $v= \sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2+(\frac{dz}{dt})^2}$, $k=\frac{\rho A}{2M}$ and $M$ is the mass of the ball.
The drag force always operates in the opposite direction to the ball's motion. So as the ball rises and curves through the air, the drag force affects the motion in all three dimensions (indicated by the presence of the drag coefficient $C_d$ in the equations of motion in the $x, y$ and $z$ directions). However, in this particular example we have assumed the ball is spinning on a vertical axis, meaning that the Magnus force only affects motion in the horizontal plane, and the coefficient $C_m$ only appears in the equations of motion in the $x$ and $y$ directions. (You can read all the details of this model in the paper in the Modelling the flight of a soccer ball in a direct free kick by Ken Bray and David Kerwin in the Journal of Sports Sciences, Vol 21, pp 75-85, February 2003.)
Solving these differential equations is not a trivial task. There are no known solutions such that the ball's co-ordinates, x, y and z can be expressed as exact formulae. Instead the equations must be solved using numerical approximations, but this is no great hardship given the many commercial software packages now available — solutions to any desired accuracy can be obtained in fractions of a second on a conventional PC.
A more practical problem is what values of $C_d$ and $C_m$ should be used in trajectory modelling. Until relatively recently very little was known about drag and spin properties for footballs but there are several ways of obtaining accurate values. One involves mounting a football in a wind tunnel, using a sensitive balance to measure the drag and lift forces as air flows around the stationary ball. The coefficients $C_d$ and $C_m$ follow immediately from equation 1 (the general v-squared equation), since the velocity, $v$, of the air stream in the wind tunnel is accurately known.

Ball launchers are increasingly used in these experiments
Another approach, much like Tait's in principle, is to measure the actual trajectory of a moving football. This can be done by recording the flight using fast, digital cameras in a rectangular volume whose dimensions have been accurately measured. The ball images in each camera's view are digitised to give a number of independent, two-dimensional data sets. These datasets are then re-constructed mathematically using a device called a direct linear transformation (DLT) to generate the implied three-dimensional co-ordinates. The differential equations in (2) are solved numerically using varying values of $C_d$ and $C_m$ until the closest possible agreement is achieved between the theoretical and measured trajectories. The values that give the closest match are taken to be the most accurate values of $C_d$ and $C_m$.
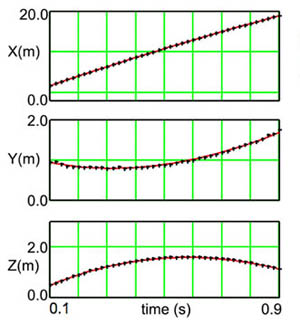
Model versus experimental data: the red line shows the modelled trajectory, and the black crosses show the trajectory measured in experiment.
An important assumption is that these parameters should remain constant over the complete trajectory. Fortunately, this is true provided the ball moves above a critical speed, about 12 mph for a soccer ball. Free kicks are taken at speeds above 60 mph and since not much speed or spin is lost during the flight the assumption is safe. Some indication of the accuracy attainable can be gained from this figure (on the left) which compares a measured and modelled trajectory. These results were obtained by using a human subject to deliver the kicks, but we increasingly use a ball launcher for this purpose. It can be programmed to deliver any speed of 'kick', with any desired orientation of the ball's spin axis.
It might be free, but it's not so easy...
Whilst modelling the flight of a soccer ball is mathematically rewarding, there are also practical implications. By including an exact mathematical description of the defensive wall in the model it is possible to study alternative strategies for this important set piece in football. For example, in the English Premiership, only about 10% of direct free kicks are successful. When games have reached defensive stalemate it is often a well-taken free kick that decides the outcome, so how can the ratio be improved?
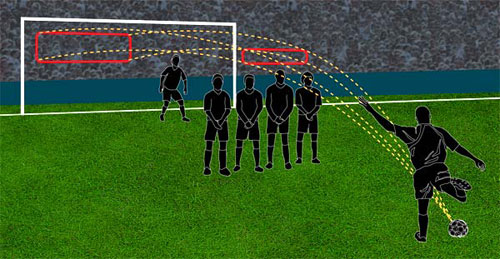
The striker must hit a 'letter box' that is just 6 football-widths wide at the defensive
wall, in order to score a central free kick from 25 yards.
The first point for players and coaches to appreciate is just how demanding the skill is to perform. Even with defenders set in a tight wall to block the intended shot, the undefended portion of the goal (seen in the figure above) may still seem like an easy target. But to hit this, the striker must place the ball within narrow limits as it crosses the defensive wall position.
This is because the horizontal deflection (caused by the sidespin of the ball) becomes greater and greater as the distance increases, so a small error in placement at the wall distance is amplified by the time the ball reaches the goal line. And it is no easier when the vertical dimension is considered. To bring the ball down in time it must not cross the wall too high, which means tight control of the speed and initial elevation of the shot. In fact, the striker is attempting to slot the ball through a 'letter box' of extraordinarily small dimensions just above the wall. For a central free kick from 25 yards this measures just over six ball-widths in length and is a little over a ball diameter high. As the angle of the free kick moves away from the central positions so the letter box shrinks in width and placement accuracy becomes critical. Many free kicks are wasted in practice because players attempt direct shots from impossible angles when playing the ball to a colleague running in for a header at goal would be tactically more astute.
Keeping their eye on the ball...

The Teamgeist has a distinctly different construction from past footballs, with only 14 panels.
Future research in this field is likely to look much more closely at the ball's specific aerodynamic properties, its surface structure and panel pattern especially. Strange things were reported about the ball used for the 2006 World Cup, the Adidas Teamgeist. This is probably the most technologically advanced object ever to have been kicked around a football pitch, yet goalkeepers complained about its erratic behaviour before the tournament and television cameras captured their horrified expressions as the ball swerved unpredictably in its passage to the goal.
The problems occur when the ball is kicked with very low spin rates, an effect easily observed in practice if the ball markings are studied in the many slow-motion replays of spectacular shots and goals. The cause may well be the Teamgeist's much reduced panel structure — 14 panels rather than the 32 of the conventional hexagon pattern ball — and the correspondingly low seam density (see the Plus news story Eye on the ball for an explanation of these effects).
Chaotic behaviour like this is not revealed by models such as the one described above (in (2)) which rely on the aerodynamic parameters not changing as the ball progresses smoothly along an orderly trajectory. More incisive analysis is required to understand such behaviour and researchers resort to sophisticated computer packages involving computational fluid dynamics (CFD) to crack these problems. Using such techniques the flow of air around the ball can be simulated in great detail and the aerodynamic forces caused by conventional spin, or discrete disturbances triggered by the panel or seam patterns, can be accurately predicted.
Such work may lead to the definition of an aerodynamic standard for soccer balls, stipulating the tolerances for the amount of swerve produced by a given speed and spin rate. The controlling authority for world football, FIFA, issues specifications for every conceivable property of the ball such as weight, sphericity, recoil in a bounce and water absorbency, but as yet there are no such specifications for the aerodynamic properties. The ball can swerve or bob about unpredictably in flight as much as the aerodynamic forces allow.
Football supporters probably feel that players like David Beckham do their talking with their feet but mathematicians may demur; there is one great challenge left. All of the methods I have described, from Tait's rudimentary approach, to the complexity of computational fluid dynamics, derive ultimately from one of the great unresolved problems of mathematical physics, the Navier-Stokes equations. Since the mid-19th century these have defied exact solution and are one of the seven Millennium Problems identified by the Clay Mathematical Institute. Solve the Navier-Stokes equations and you can claim a prize of $1 million (find out more in How maths can make you rich and famous II). It is sobering to think that whilst this outcome would set the world of mathematics on fire, the prize would not pay the wages of a middling professional footballer for longer than half the playing season!
About the author

Ken Bray is a theoretical physicist and a Visiting Fellow in the Sport and Exercise Science group at the University of Bath. His first book How to Score - science and the beautiful game was published by Granta in 2006 and is reviewed in this issue of Plus.
Comments
Chuck
Ken, can you comment on how creating spin adds an element of feel and control to shots that isn't present when contact is more square on?