
The dynamic sun

The Sun, our nearest star, provides all the light and heat needed for life on Earth. It is no wonder that ancient civilisations worshipped it as a god.
On 11th August 1999 a total eclipse of the Sun will be visible from parts of the UK.
It will provide a spectacular display, but why is the Sun so interesting?
What is a total eclipse of the sun?

Figure 1: Solar corona at eclipse, 3 Nov. 1994, Putre, Chile. (Photo c/o High Altitude Observatory, NCAR, Boulder, Colorado, USA.)
During a total eclipse, the moon completely blocks out the solar disc. In figure 1, what you see is the corona (which means crown), the Sun's outer atmosphere.
It's very difficult to see the corona normally because the visible light from the solar surface, the photosphere, is a million times brighter than the light from the corona.
Where will the August 11th 1999 eclipse be visible?
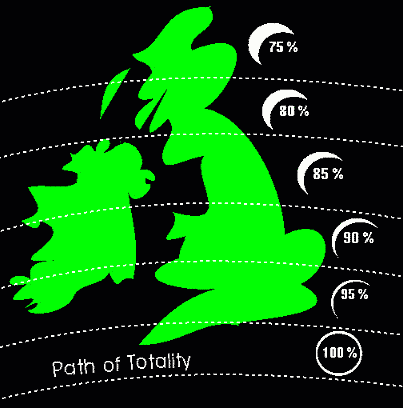
Figure 2: Viewing regions for the August 99 eclipse
The sketch map in figure 2 shows whether the eclipse will pass your way. Of course, to really experience this event you need to be in the path of totality (the region on Earth where the Sun's disc will be seen as fully obscured by the Moon's). This is never more than 300 km wide, and since not everyone in the UK can fit into Cornwall, some of you will have to watch the full effect of the eclipse on TV.
Remember, always use a special filter to look at the Sun or you will damage your eyes.
This will be the final total solar eclipse of the 20th century.
What else can you see during an eclipse?

Figure 3: Pinhole images on a car in Guadeloupe.
During the first moments of the eclipse, the Moon begins to block out the Sun's disc. It looks as if a "bite" has been taken from the edge of the Sun. The photo in figure 3 was taken during the 1998 eclipse in Guadeloupe. You can see many images of the crescent Sun. The gaps in the tree's foliage act like tiny pinhole cameras. Each one focuses an image of the Sun onto the car.

Figure 4: Baily's Beads.
The images in figure 4 show what are called Baily's Beads at the end of a total eclipse of the Sun. Baily's Beads are actually caused by rays of light from the Sun's surface, photosphere, shining along crevices on the edge of the Moon.
How hot is the solar atmosphere?
Although the photosphere is a cool 6000 C, the corona (the outer atmosphere) is very, very hot - over 1,000,000 C! This problem has puzzled solar physicists for more than 50 years. There are several theories as to why this should be so, none yet fully satisfactory.
The corona could be heated by waves travelling up from the photosphere. We know that the magnetic field plays an important role, so magnetic re-connection could transfer magnetic energy into thermal (heat) energy.

Figure 5: X-ray image from the SXT instrument on YOHKOH, a Japanese satellite (ISAS/NASA/UK).
If you look at the Sun in X-ray emission, as in figure 5, you see only the plasma (ionised gas) at above one million degrees. You can clearly see the structure of the magnetic field.
The Sun generally has a dipole magnetic field (like a bar magnet). The field lines are open in the polar regions and the corona flows out to form the "fast" (700 km/s) component of the solar wind.
In the equatorial region, the magnetic field is closed and we see bright hot loops of trapped plasma, called active regions. These are locations where sunspots, regions of very strong magnetic field, are seen in visible light. The active regions stretch out into streamers which are the source of the "slow" (400 km/s!) solar wind.
What is SOHO?
The Sun may appear tranquil but actually it is an incredibly dynamic object with violent explosions spitting out millions of tons of material towards us at high speeds. We are able to watch the Sun twenty four hours a day with a satellite called SOHO - the Solar and Heliospheric Observatory. (SOHO has already made an appearance in PASS Maths: see Mathematical mysteries: the three body problem in issue 6).
Launched in December 1995, SOHO, an ESA/NASA project, carries many instruments to study the solar interior, the atmosphere and the solar wind. SOHO monitors different types of radiation from the visible to the ultraviolet.
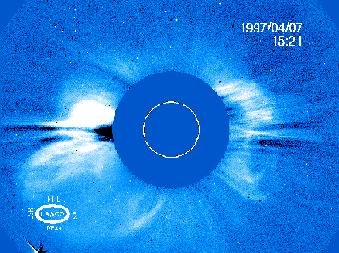
Figure 6: Image from SOHO's LASCO coronagraph.
Figure 6 shows an image taken by the LASCO coronagraph on SOHO, which simulates a total eclipse of the Sun. The white circle shows where the Sun's disc should be (if it were not blocked out). Plasma, called a coronal mass ejection, is shot out into the solar wind and can impact on our own terrestial environment, causing problems with satellites, radio blackouts and disruption to electricity supplies. This is what we call space weather.
The Sun and waves
Waves play a very important role in the Sun. The Sun emits not just visible light, but light from all across the electromagnetic spectrum - from radio waves to UV, X-rays and gamma-rays. There are two types of waves. In transverse waves, like the waves produced by wiggling a rope or on the surface of water, the direction in which the rope or water moves is at right angles to the direction in which the wave moves. On the other hand, sound (acoustic) waves are an example of a longitudinal wave. As the wave moves along, the molecules of air move backwards and forwards in the same direction as the wave.
Wave Equation
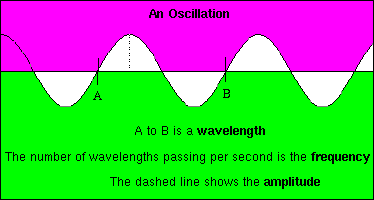
Figure 7: Features of a sine wave.
Waves all obey the equation $$ v = f\lambda $$ where $v$ is the speed of the wave, $f$ the frequency, and $\lambda$ the wavelength. The amplitude, $a$, of the wave is the maximum displacement (shown in the diagram). \par Electromagnetic waves travel at the speed of light, which is a constant, $c = {3 \times 10^8}$ m/s. The speed of sound depends on the properties of the medium through which the wave travels. \par The wave motion can be described mathematically as: $$ y = F\left(x - {vt}\right) $$ where the wave is moving with a constant speed $v$ in the direction $x$ at time $t$, and $F$ is any arbitrary function. \par The simplest example of a wave is a {\em harmonic} wave in which the wave shape is a sine or cosine curve. $$ y = a \cos\left(\frac{2{\pi}}{\lambda}\left(x - {vt}\right) \right) $$ \par All these waves are solutions of the second order differential equation $$ {d^2y\over dt^2} = v^2{d^2y\over dx^2} $$ Check this for yourself! (Properly, this equation should be a so-called "partial differential equation", but we don't need to worry about that here.) \par The time taken for one complete wave to pass any point is called the {\em period}, $T$, of the wave ($= {\lambda/{v}}$). \par The frequency of the wave, $f$ is the inverse of the period ($= {1/T}$).
Doppler Shifts
If we measure light from an object that is moving towards us, the wavelength of the light changes from $\lambda$ to $\lambda\left(1-\left(u/c\right)\right)$, where $u$ is the speed of the object moving toward us. This shift in the wavelength (or frequency) is referred to as a {\em Doppler shift}.
You'll hear this same effect with sound waves, when a car speeds around a race track, towards and then away from you. This effect has been used to study the ultraviolet spectrum from the solar atmosphere with SOHO. We have discovered solar tornadoes on the Sun and located the source of the fast solar wind.
Standing Waves
Standing waves can be produced with a taut string fixed at both ends. Another example can be found with sound waves in a musical instrument, a guitar or flute.
Standing waves result from the interference of two sets of waves of the same frequency, passing through each other in opposite directions. This is usually incident waves and reflected waves. The resulting wave pattern remains fixed in space. The wave amplitude varies from zero ({\em nodes}) to a maximum, half way between the nodes. For a string of length $L$, the longest wavelength (lowest frequency), called the {\em fundamental mode}, is $\lambda = {2L}$. \par A solution of the differential equation which describes a standing wave has the form: $$ y = \sin\left({m {\pi} x}\over{L}\right) . \left[a \cos\left({ {m {\pi} v t}\over{L}}\right) + b \cos\left({{m {\pi} v t}\over{L}}\right)\right] $$ This solution is called a {\bf normal mode} of vibration of the string. There are an infinite number of these modes corresponding to {\em m = 1, 2, 3,} etc ({\em m = 1} is the fundamental mode).
How does SOHO see inside the sun?
Seismology is the study of earthquakes and is done by measuring the vibrations of the Earth's surface. Helioseismology is a comparatively new field of solar physics (begun in the 1970s) whereby vibrations of the Sun's surface are measured (Helios is the Greek word for Sun).
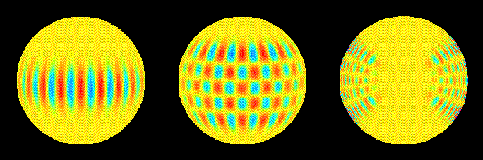
Figure 8: P-modes on the solar surface.
The vibrations arise through the presence of standing waves in the Sun's interior. In the Sun, we get 3-dimensional standing waves. The solar oscillations near the surface are called P-modes. Figure 8, courtesy of the solar centre at Stanford, shows some calculations of the patterns formed by different P-modes on the solar surface. The blue and red patterns show where the amplitude of the waves on the surface is largest (moving in opposite directions). The background yellow is where the surface isn't moving (nodes).
The waves cause the surface of the Sun to move up and down by small amounts, at a fraction of one km/s. We can detect these small motions by looking at the Doppler shift in spectral lines emitted by atoms in the solar surface. These movements can be compared to how the Sun is expected to behave from standard theoretical models.
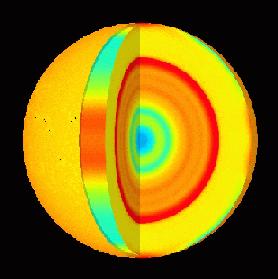
Figure 9: Image from SOHO's MDI instrument.
The image in figure 9 was produced from observations by the Michelson Doppler Imager (MDI) instrument on the SOHO satellite. It shows the difference between the calculated and predicted speed of sound waves, inside the Sun. In red coloured layers, sound travels faster than predicted by theories. The blue colour means that sound travels slower than expected.
The red layer at about one third of the way down from the surface to the centre of the Sun is thought to be a shear layer just below the solar convection zone. It seems that there may be a lot more turbulence there than predicted.
The blue layer in the core of the Sun indicates that the temperature may be 0.1% cooler than the expected 15 million degrees C. Although this may seem a very small difference, it suggests that the power produced by nuclear fusion may be lower than expected, in fact that it may vary over long time periods.
What is Sun Block '99?
 |
 |
 |
Sun Block '99 is a web-site with solar images and movies from SOHO and other solar space observatories. It is aimed at secondary school children (aged 13-16 years) and has been produced by a team of solar scientists and teachers.
At the Sun Block '99 site, young solar researchers, from all over Britain, communicate some fundamental scientific principles in a fun and interesting manner.
The SB99 project is produced by a team from the Rutherford Appleton Laboratory and the Universities of St Andrews and Cambridge, together with educational consultants. It has, in part, been sponsored by PPARC and the Millennium Mathematics Project.
To explore Sun Block '99, link through to:
http://www.sunblock99.org.uk
About the authors

She has worked on many solar space projects, including Skylab, the Solar Maximum Mission, Spacelab and more recently SOHO. She has taught physics and maths for London, Cambridge and the Open Universities.
Helen has written popular articles, given public lectures, participated in radio and TV programmes, and is the science editor for the Sun Block '99 project. PASS Maths had an article on her career in Issue 1.

Dr Peter Young is a post-doctoral researcher at DAMTP. He is studying the ultraviolet light from the Sun's atmosphere observed by SOHO.
He was born in Northumberland and became interested in astronomy when he was about 8 or 9. He studied science and maths at Cambridge University. He is part of the Sun Block '99 team.
He loves to travel and has been to America to work "hands-on" with the SOHO satellite as well as visiting France, Italy and Germany.