The 36 officers problem

This article is part of Five of Euler's best. Click here to read the other four problems featured in this series, which is based on a talk given by the mathematician Günter M. Ziegler at the European Congress of Mathematics 2016.

This problem looks like a puzzle you might find in a Sunday paper. Imagine there's a war. You're in command of an army that consists of six regiments, each containing six officers of six different ranks. Can you arrange the officers in a 6x6 square so that each row and each column of the square holds only one officer from each regiment and only one officer from each rank?

Just as any Sunday puzzler Euler had a go at the problem, but without success. "After we have put a lot of thought into finding a solution, we have to admit that such an arrangement is impossible, though we can't give a rigorous demonstration of this" he wrote in 1782. A proof that the problem is impossible to solve didn't come along until nearly 130 years later. The French mathematician Gaston Terry provided it in 1901.

If you've ever come across Latin squares, then the 36 officers problem might have reminded you of them. A Latin square is a square array of symbols (for example numbers or letters) in which every symbol occurs just once in every row and column. If you combine two Latin squares of the same size but with different symbols, you get what's called a Graeco-Latin square (also called an Euler square). It contains pairs of symbols so that every member of a pair occurs exactly once in each row and column, and so that every possible pair appears exactly once on the array.

+

=

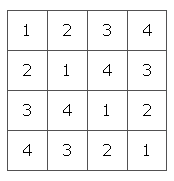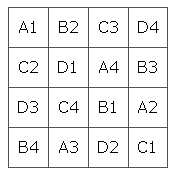Euler realised that a solution of the 36 officers problem would give us a Graeco-Latin 6x6 square. The pairs in this case represent an officer's rank and regiment. That's unlucky: if their had been five regiments and ranks, or seven regiments and ranks, then the problem could have been solved. Euler was aware of this too and speculated that Graeco-Latin squares are impossible if the number of cells on the side of square (the order of the square) is of the form 4k + 2 for a whole number k (6 = 4x1 +2). It wasn't until 1960 that he was proved wrong. The mathematicians Bose, Shrikhande and Parker enlisted the help of computers to prove that Graeco-Latin squares exist for all orders except 2 and 6.

So why do we mention what at first sight looks like an Euler fail rather than an Euler success? Because as usual with Euler, there's a lot more to his work on the problem than a bit of speculation. The 36 officer problem inspired him to a lot of work on Latin and Graeco-Latin squares, including on problems akin to modern-day sudoku (see this article for more on sudoku and other types of interesting squares). It contributed important work to an area of maths called combinatorics which, as you may have guessed, is about combining objects in ways that satisfy particular constraints, and has many applications in the real world.

About this article

This article is part of Five of Euler's best. Click here to read the other four problems featured in this series, which is based on a talk given by the mathematician Günter M. Ziegler at the European Congress of Mathematics 2016.

Günter M. Ziegler is professor of Mathematics at Freie Universität Berlin, where he also directs the Mathematics Media Office of the German Mathematical Society DMV. His books include Proofs from THE BOOK (with Martin Aigner) and Do I count? Stories from Mathematics..

Marianne Freiberger is Editor of Plus. She really enjoyed Ziegler's talk about Euler at the European Congress of Mathematics in Berlin in July 2016, on which this article is based.