And the Nobel Prize in Mathematics goes to...

No-one won the Nobel Prize for mathematics in 2010 ... because there isn't a Nobel Prize for maths. Some have speculated that Alfred Nobel neglected maths because his wife ran off with a mathematician, but the rumour seems to be unfounded. But whatever the reason for its non-appearance in the original Nobel list, it's maths that makes the science-based Nobel subjects possible and it plays a fundamental role in many of the laureates' work. Here we'll have a look at two of the prizes awarded this year, in physics and economics.

The Nobel Prize in physics

Andre Geim. Image Prolineserver.

The Nobel Prize in physics went to Andre Geim and Konstantin Novoselov for their discovery in 2004 of a material called graphene, which no-one believed could actually exist. Graphene is the thinnest material that's ever been found — it's made up of a single layer of carbon atoms locked together in a honeycomb lattice. If you stack 3 million layers of graphene on top of one another you get a layer of graphite, the material you find in ordinary pencils, that's only 1mm thick. The strong bonds between the atoms in graphene make it incredibly robust. Apparently, if you manage to balance a pencil on its tip on a sheet of graphene and then manage to balance an elephant on top of the pencil, the pencil still won't puncture the sheet.

While strong, the bonds between atoms are flexible enough to allow the lattice to stretch by up to 20% of its original size. And as if that wasn't enough, graphene is the best conductor of heat known to science, an extremely good conductor of electricity and very nearly transparent. The unusual properties of graphene had already been predicted theoretically as early as 1947, but no-one believed that such a thin material could actually exist in reality. Geim and Novoselov first managed to produce it by ripping layers off graphite using adhesive tape.

Konstantin Novoselov. Image Prolineserver.

With its amazing properties, the list of potential applications of graphene is truly impressive. Mixing it in with other substances we may be able to produce super-strong but elastic and leightweight composite materials for aircraft, satellites and cars. It could be used to make transparent touch screens and flexible, wafer-thin computer monitors you can fit in your pocket. Graphene could replace sillicone as the material from which to make computer chips, with the unusual behaviour of electrons in graphene leading to ever faster and efficient computers. A graphene transistor that's as fast as its sillicone counterpart has already been built a few years ago.

The most exciting application of graphene, however, has little to do with gadgets, or at least not directly. It goes straight to the heart of theoretical physics. It turns out that the interaction between graphene electrons and its special lattice structure means that the electrons behave very similar to photons, the particles that make up light. Similar to photons, which have no mass at all, the electrons in graphene also behave as if they had absolutely no mass. Their behaviour is therefore governed by the Dirac equation, which gives a quantum-mechanical description of electrons moving relativistically, that is near the speed of light. The electrons travelling in graphene move at a constant speed of one million meters per second. And this speedy behaviour may give ways of testing for strange relativistic phenomena, which are predicted by the underlying mathematical theory but have never been observed, without having to build large and expensive particle accelerators.

Graphene is a honeycomb lattice made of carbon atoms. Image AlexanderAIUS.

One strange effect that graphene may shed light on involves something called quantum tunnelling. Sometimes physical particles perform feats that require levels of energy the particle doesn't actually have. This happens, for example, in a certain type of radioactive decay (known as alpha-decay), where the decay process requires more energy than the decaying atom has available (see Play the quantum lottery for more information). Acquiring energy from out of nowhere violates the laws of classical physics, but it's explained by quantum mechanics. Loosely speaking, quantum mechanics says that when you look at a physical system over very, very small time scales, the information you have about the energy in the system becomes hazy. This isn't because your tools to measure the energy are too imprecise, but because there is inherent uncertainty: there isn't one true value for the energy in the system, but a whole range of possible values, each of which the system's energy could take with a certain probability. Thus, there is a real chance — a non-zero probability — that for a split second the system acquires more energy than it should have according to classical physics.

This process is called quantum tunnelling because it's akin to a particle sitting at the foot of a mountain — the energy potential barrier — which it doesn't have enough energy to climb. Quantum mechanics allows the particle to tunnel into the mountain instead, and possibly to emerge on the other side. For ordinary particles, the probability of tunnelling decreases exponentially with the height of the barrier. However, the Swedish physicist Oskar Klein showed in 1929 that the underlying mathematics predicts something very different for relativistic particles. Here the tunnelling probability actually increases with the height of the barrier, until for very high barriers the mountain becomes completely "transparent" for the particle.

A levitating frog. Image: Lijnis Nelemans.

This mathematical fact is so counter-intuitive that people called it the Klein paradox. It's never been observed in reality because creating a high enough barrier would involve a super-heavy nucleus or even a black hole. However, Geim, Novoselov and their colleagues have shown that using the massless electrons in graphene, it should be much easier to create the effect. If the effect doesn't materialise, then something is wrong with the theory of quantum mechanics.

Geim is no stranger to scientific accolade. In 2000 he and his colleague Sir Michael Berry received the Ig-Nobel Prize for improbable research for using magnets to levitate a frog. Geim is the first person to have received both prizes — congratulations!

The Prize in Economic Sciences

Peter Diamond. Image: MIT.

Economical models can be perplexingly simplistic. The classical view of markets, for example, assumes that buyers and sellers have no trouble finding each other and have perfect information about all the prices and goods that are available. But if you've ever sold a house or changed jobs, you know that this couldn't be further from the truth. Finding a potential buyer or new job is expensive in terms of both time and money, and even when you've found one there's no guarantee the deal will come off. This year's laureates of the Prize in Economic Sciences, Peter Diamond, Dale Mortensen and Christopher Pissarides received their price for developing a mathematical theory that takes account of such frictions in the market. In particular, they've developed a mathematical model for the labour market, known as the DMP model, which gives insights into how unemployment depends on various factors, such as hiring and firing cost, the level of unemployment benefits and the efficiency of recruitment agencies.

Dale Mortensen.

The DMP model incorporates several components describing features such as wage negotiation, the decision of companies to create new jobs, just how much a given job is worth to the employee and the overall flow of the labour market.

As an example of how features like these can be captured mathematically, think of the labour market as a whole. Assume that there are $N$ workers on the market, each of whom can be either employed or unemployed. Suppose that as time goes by, all employed workers lose jobs at the same rate, which is reflected in a constant job destruction rate $\phi$ . The rate at which unemployed workers find jobs is given by a function $\alpha (V/U)$ . It depends on the ratio $V/U$ , where $V$ is the number of vacancies and $U$ the number of unemployed people. The function $\alpha$ increases with $V/U$ , that is the more vacancies there are per unemployed worker, the easier it is to get a job. The function is constructed in a special way so that it also describes the frictions in the labour market, that is the ease (or lack of it) with which workers and employers find each other.

Christopher Pissarides. Image: Nigel Stead/LSE.

Now if nothing drastic happens to the market, it eventually settles in an equilibrium with a constant rate of unemployment. In other words, the flow of workers from employment to unemployment equals the flow of workers from unemployment into employment. The first of these two quantities can be written as $\phi (N-U)$ , where $N-U$ is the number of employed people. The second quantity can be written as $\alpha (V/U)U$ . If the market is in equilibrium, then the first equals the second, so

$\phi (N-U)= \alpha (V/U)U.$

From this we can work out the equilibrium unemployment rate $U/N$ :

$U/N=\frac{\phi }{\phi +\alpha (V/U)}.$

This equation describes how the equilibrium unemployment rate depends on the job destruction rate $\phi$ and the job-finding rate $\alpha$ . Since $\alpha$ also reflects frictions in the market, we can see how these frictions effect the equilibrium unemployment rate.

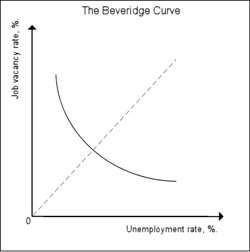
The Beveridge curve. Image from Wikipedia.

Interestingly, this component of the DMP model also gives a theoretical explanation for a relationship that has long been observed empirically. As an economy goes through the usual cycle from relative boom to relative bust, its equilibrium unemployment rate, as well as the vacancy rate (the number of vacancies per worker), change. If you plot unemployment rate against vacancy rate at various points in the cycle, you find that the points you get trace out a curve with a distinctive downward sloping shape, known as the Beveridge curve (after William Beveridge, whose work served as a foundation for the welfare state). The curve indicates that high unemployment goes with fewer vacancies and vice versa. The equation we found above relates the equilibrium unemployment rate to the job-finding rate $\alpha$ , which in turn depends on the number of vacancies $V$ . You can re-write this equation to relate the unemployment rate to the vacancy rate. If you then plot the graph for this relationship (for a fixed $\phi$ and $\alpha$ ), you get a Beveridge curve, which has been observed so many times in real economies.

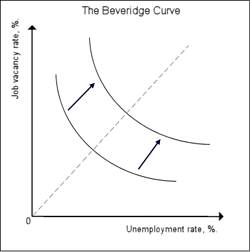
The Beveridge curve of an economy can shift its location. Image from Wikipedia.

But while an economy can slide along such a curve as it goes through the business cycle, it can also shift to another curve with the same shape. According to our equation, this corresponds to a change in the job destruction rate $\phi$ or the friction in the labour market, as reflected in the function $\alpha$ . Thus, if an economy jumps from one Beveridge curve to another, you know that something fundamental has changed in the workings of the labour market. For example, there may have been a fundamental shift in technology leaving companies with a skill shortage as workers have not yet caught up with the change. In that case, the curve will shift upwards and to the right: for the same number of vacancies there now are more unemployed workers, since many of them lack the new skills. So while an economy's position on the Beveridge curve indicates where it is in the business cycle, the location of the curve as a whole reflects how well the labour market itself is working.

This model of the flow of labour in the market is just one component of the larger DMP model. The search and matching theory developed by Diamond, Mortensen and Pissarides is now the predominant model to study the effect of social economic policies, including unemployment benefit. One of its predictions is that high benefits lead to higher unemployment and a longer search time for job seekers — perhaps not entirely unsurprisingly. The theory doesn't only apply to the labour market, but can also be used to understand a range of other social phenomena.