As the Wimbledon 2011 Championships hove into view, memories will be reawakened of the match of epic proportions that took place last year between the American John Isner and the Frenchman Nicolas Mahut. Like a couple of Titans banished to Tartarus for an eternal bat'n'ball battle, these two men slugged it out for a touch over 11 hours, spread over three days, even causing the scoreboard to temporarily give up the ghost. In the end Isner prevailed 6-4, 3-6, 6-7, 7-6, 70-68. This smashed the previous fifth set record of 21-19 when Andy Roddick beat Younes El Ayanaoui in the 2003 Australian Open, and sundry other records besides.

So just how freaky was this fifth set and what odds might a bookmaker offer for a repeat? I will be using men's singles matches at Wimbledon for the frame of this article. Women's matches are far less likely to produce marathon sets because the serve is much less dominant and doubles don't feature as greatly in the public consciousness these days.

It's all in the serve

Huge set scores are only possible when the tie-break system is not being employed to decide who wins a particular set. Tie-breaks tend to be the norm these days, but notable exceptions include the final set of matches at Wimbledon, the Olympics and the Australian and French Opens. In these tournaments final sets are won by the first player to win six games, unless the game score reaches 5-5, when a player needs to get two clear games ahead (ie 7-5, 8-6, etc) to win the set. From game to game players take turns in serving the ball. A very long set occurs when both players keep winning their service games for a long time before someone manages to "break" their opponent's serve. A phenomenal set score is therefore only possible if the players are evenly matched heavyweight servers, so that the probability of a break of serve is small.

To investigate the set, we need to construct a probabilistic model of some kind. The most obvious thing to do is to treat the constituent games of the set as Bernoulli trials. These are independent repeated actions (in this case games), where there is a definite probability of success and failure. We can then calculate the likelihood of seeing such a massive string. Clearly, there are two types of game/trial, one for each server. I'll assign "success" to the outcome of the server holding serve.

Point...

The games themselves are composed of a series of points, which in turn can be treated as Bernoulli trials. It's not straightforward how we should go about getting figures for the probability of a player winning a point on their serve, despite the wealth of statistics available these days. We could look at the players' previous encounters but Isner and Mahut had met just once two years prior, since when Isner had significantly improved. We could take the data from the match itself (available on the Wimbledon website) and work backwards but this data unfortunately includes the fifth set, so this method is open to the accusation of circularity – you're using the very data you're trying to give an explanation for. If you start out weird, you'll end up weird but within that closed weird system, it will appear normal.

What I propose we do is use a combination of the Isner-Mahut data and data from a few other recent five set matches at Wimbledon between well-matched heavyweight servers. Now, the serving points won % for John Isner and Nicolas Mahut was 76.2% and 78.7% respectively, but from my casual look at other data, the low seventies seem to be more the norm. So, remembering that we're interested in the general case, let's keep things simple and assert that:

$$Prob(\mbox{Either player wins a point on their serve})=p=0.75.$$

This is our starting point from which everything proceeds.

...Game...

We can now derive the probability $P$ that a player holds serve. We'll assume independence between points, in other words that the event of one point being scored has no bearing on any other point being scored. A game is won by the first player to win 4 points, unless the score goes to 40-40 (corresponding to both players having won 3 points). This situation is called a deuce and a player needs to win two consecutive points to win the game from deuce. So the server can hold serve by winning a game to zero points (love), to 15, to 30 or via any number of deuces, giving \begin{eqnarray}\nonumber P & =& Prob(\mbox{Hold serve to love})+Prob(\mbox{Hold serve to 15})\\ &+&Prob(\mbox{Hold serve to 30})+Prob(\mbox{Hold serve via deuces}).\end{eqnarray} The probability that a game is won to love is simply $p^4$. If a game is won to 15, then the server scored four points (probability $p^4$) and the receiver scored one point (probability $(1-p)$). The receiver's solitary point must come somewhere in the first four points, before the server clinches the game with the next point at 40-15. There are four ways in which this can happen (the opponent can score their point first, second, third, or fourth), so the probability of the game being won to 15 is $$Prob(\mbox{Hold serve to 15})=4p^4(1-p).$$ Similar reasoning gives $$Prob(\mbox{Hold serve to 30})=10p^4(1-p)^2.$$ The game goes to deuce when both players have scored three points. There are 20 ways in which the total of six points can be split between the players. Writing $D$ for the probability that the server wins once a game has gone to deuce gives $$Prob(\mbox{Hold serve via deuces})=20p^3(1-p)^3D.$$ To work out the probability $D$ we use a trick. If the server is to win the game from the position of deuce, he must win two consecutive points, either immediately or after some number of deuce cycles. The probability of him winning immediately is $p^2$. Else both of the players win a point one after the other and then we are back to deuce. The probability of two players winning a point one after the other is $2p(1-p)$ (since there are two ways the points can be split between the players). Then the probability of winning from the position of deuce, but not immediately, is $2p(1-p)D.$ Putting this together gives $$D=p^2+2p(1-p)D.$$ Solving for $D$ gives $$D=\frac{p^2}{1-2p(1-p)}.$$ This gives $$Prob(\mbox{Hold serve via deuces})=\frac{20p^5(1-p)^3}{1-2p(1-p)}.$$ Plugging $p = 0.75$ into equation 1 we find: $$Prob(\mbox{Either player holds their serve})=P=0.95 \;\;\;\mbox{(rounded to two decimal places.)}$$

As you'd expect, the probability of the server winning his service game far outstrips that of him winning a single point on his serve (incidentally, this is also the reason why a best of five set match is more likely to be won by the better player than a best of three set match). In broad terms then, we would expect a service break in about 5% of games, that is once in every 20 games (corroboration of this might be taken from the first four sets, where there were two breaks in 43 games).

We must comment on the huge caveat of assuming independence between the points. By doing this, we are treating the players as relentlessly consistent automatons, which is clearly not the case. A more sophisticated model would look to build in conditional probabilities that take account of the in-game score (for instance, should the server lose the first point, $p$ might fall due to added pressure) or even "catastrophes", where the server just loses it and $p$ plummets, resulting in a significantly different value for $P$.

More specifically to this match, it has been suggested that increasing fatigue favours the server over the receiver. This would imply that the probability of a player winning a point should change as the set progresses. But I'm not completely convinced by this. Could there also have been some subtle transformation from sportsmen to actors as the set wore on, a grand collusion to extend their fifteen minutes of fame? Whatever, it must be acknowledged that the model is hopelessly inadequate to account for the technical peculiarities and emotional swells and falls of the players.

...Set...

We could treat the set in a similar fashion as we did a game, which would mean calculating the probability that the set ends normally by six games to something (the analogue of a non-deuce game), and then calculating the probability that the set ends in successive two-game increments should the score reach 5-5 (the analogue of the deuce cycle at game level, i.e. you've got to win by two clear units of action).

However, because we know that the probability of a break is pretty small, we can use the time to first break (measured in games) as a proxy measure for the end of the set. This will give a slight underestimate of the probability because the possibility of consecutive exchanged service breaks is not accounted for (this occurred in the Roddick-El Ayanaoui fifth set before the decisive break later on) but it's not significant for ballpark calculations.

The time to first break is a random variable $X$ where the probability of the first break occurring in the $nth$ game is given by $$Pr(X=n)=P^{n-1}(1-P).$$ (Recall that $P$ is the probability of a player holding their serve.) This probability distribution is known as the geometric distribution because the sequence of probabilities $Pr(X=n)$ for $n=1,2,3...$ forms a geometric progression with first term $(1-P)$ and common ratio $P$. The probability of the first break having occurred by or at the $nth$ game (the cumulative distribution of $X$) is given by $$Pr(X \leq n) = 1-P^n.$$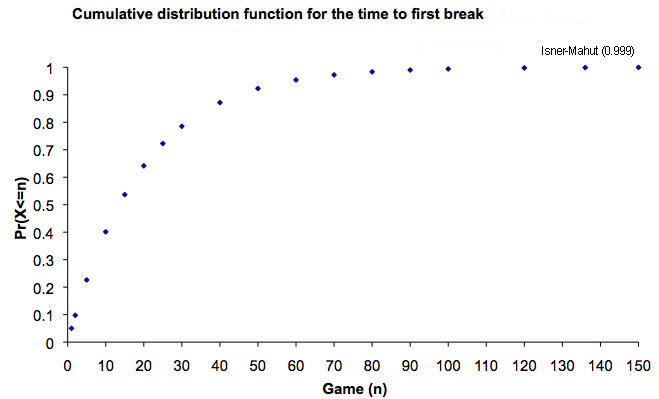

...And mega set

We can now calculate the probability of a Isner-Mahut set by plugging $n=136$ into $$Pr(X>n)=P^n.$$ This returns about a 1 in 1000 chance with liberal rounding. The result is exquisitely sensitive to the value of $P$ and hence, working backwards, to the value of $p.$ Had we used $p=0.78$, as the Isner-Mahut match data alone suggests, this would have returned a roughly 1 in 80 chance – practically a shoo-in! Conversely, had we been a bit more conservative and posited $p=0.72$, the chance of Isner-Mahut drops to 1 in 55,000.

So, again making horribly general assumptions, if around one in five of the 127 matches played at Wimbledon in the men's draw each year go to five sets, and one in five of these are between heavyweight servers, we get a 1 in 200 chance of Isner-Mahut (since 127/5² is roughly 5 and 5/1000=1/200). Alternatively expressed, there's about a 25,000 to 1 chance that a random match in the men's draw produces Isner-Mahut. But whatever happens at this and future Wimbledon Championships, Messrs. Isner and Mahut are likely to be mutually defined until the day they die … and for some time thereafter

---

About the author

Mark Thomas has a physics background and writes about things that tickle his fancy.