Breaking symmetry

Talk to a physicist about symmetry and you'll probably see their eyes light up. Symmetry plays an important role in physics. That seems reasonable, given that many objects in the physical world — planets, people, plants — are roughly symmetrical. But physicists get equally excited about symmetry breaking. They even believe that many of the features of the world we live in are a result of it. What on Earth do they mean by that? To understand the idea, let's start with crystals.

Crystal beauty

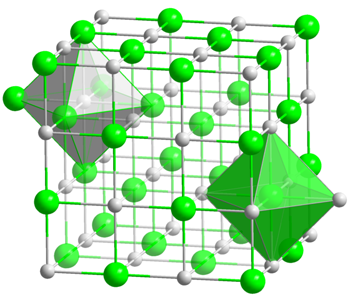
The crystal structure of table salt.

When a crystal forms, its atoms line up in a regular lattice; for example a cubical lattice like in the image on the right. Such a lattice can be tilted one way or another: the rods do not have to be vertical and horizontal, as they are in the figure. In fact, in a real crystal the lattice is not tilted in the exact same way throughout the crystal. Instead, the crystal is made up of tiny patches, called domains. In any one domain, comprising perhaps millions of atoms, the lattice is tilted in the same way. But the lattices in different domains will have different tilts.

Typically the crystal forms by cooling a sample of liquid. (Remember the blue copper sulphate crystals you made in chemistry class at school, competing for who had the gentle touch to grow the biggest one!). The atoms settling down into a lattice is an example of a ubiquitous phenomenon in physics and chemistry: a system settling down into its state of lowest energy. Just as you, when you flop down on the sofa, assume a position that takes the least energy to maintain, so physical systems naturally strive to a lowest energy state. Ideally, the crystal lattice would have the same tilt throughout the entirety of the sample. The entire sample would form one vast domain, and the energy would indeed be lowest since there would be no lines or surfaces within the crystal where the tilt changes, with an associated energy cost. But that is of course very much an ideal, that is, an unrealistic, situation. In reality, there will be a vast number of tiny events scattered throughout the cooling liquid (for example the presence of a speck of dust, or a passing cosmic ray) each of which can result in a shift in the local tilt of the lattice.

To sum up: we expect the physics and chemistry of the crystal's atoms to determine the general shape of the lattice, for example whether it is cubical, as in the picture. But we expect the exact orientation to be a matter of sheer happenstance, influenced by local events; and so it is very likely to be different, in different parts of the crystal.

There is a name for the variety in the tilts, the different tilts in the different domains: symmetry-breaking. The idea is that the physics and chemistry of the crystal's atoms, and the overall cooling process, do not prefer one tilt over any others. These principles allow the lattice any orientation in space: they have full rotational symmetry. But a specific state of the system, a specific domain, breaks the symmetry: it picks an orientation — because of microscopic causes that we may never know (nor care!) about.

Symmetric laws

This scenario, of symmetric principles having a non-symmetric instance, generalises. A law (or collection of laws) of physics can have a symmetry, while a solution to those laws lacks it — and again, not because of some mystery, but simply as a matter of sheer happenstance. Once you grasp this idea, you realise that examples are everywhere: they are two a penny.

Kicking the ball: Direction matters.

For example, Newton's laws of mechanics and his law of gravitation are rotationally symmetric. They encode no preferred orientation. If you calculate how your equation expressing these laws is transformed by rotating the coordinate system around any axis by any chosen amount (for example around the axis passing through the Earth's North Pole, by a 33 degree angle), you will find that the equation expressing the laws remains exactly the same.

On the other hand, almost all the solutions of Newton's laws are not rotationally symmetric. As an example imagine kicking a ball in the air straight ahead of you. Newton's laws enable you to calculate the trajectory of the ball — the trajectory is a solution to Newton's laws. If you rotate yourself by 180 degrees and kick the ball again, in the exact opposite direction, the ball will follow a different trajectory: you will get a different solution to Newton's laws. So although the laws themselves are rotationally symmetric, they don't change depending on which direction you are kicking a ball in, the solutions to these laws are not. When you rotate a solution, for example by kicking the ball in another direction, you get a different one.

Generally, almost all the solutions of Newton's laws are not rotationally symmetric. They are not transformed into themselves by a rotation about any axis, by any amount. That would require that the solution is spherically symmetric, like a perfectly symmetric sphere of dust. The solution breaks the symmetry enjoyed by the law. Of course, this is in no way a problem, rather it is exactly what one would expect. The instantaneous state of a collection of bodies is usually not symmetric, and the lack of symmetry is usually a matter of sheer happenstance; of historical contingency — of where the bodies happened to be placed and how they happened to be moving.

Physicists believe that the Universe as a whole has also experienced symmetry breaking. At its inception, right after the Big Bang, the Universe was symmetrical in many ways, reflecting the symmetries of the laws that govern it. But as it cooled down and expanded, various symmetries were broken, resulting in some of the features we observe today. The Higgs mechanism, which explains how the fundamental particles acquired mass (and uses the famous Higgs boson), is an example of symmetry breaking (find out more here). The imbalance of matter and anti-matter we observe in the universe is also believed to be a result of symmetry breaking (see here).

So next time you see a physicist's eyes light up at the mention of symmetry, you will know why.

About the author

Jeremy Butterfield is a philosopher of physics at the University of Cambridge.