
Secret symmetry and the Higgs boson (Part I)
It's official: the notorious Higgs boson has been discovered at the Large Hadron Collider at CERN. The Higgs is a subatomic particle whose existence was predicted by theoretical physics. Also termed the god particle, the Higgs boson is said to have given other particles their mass. But how did it do that? In this two-part article we explore the so-called Higgs mechanism, starting with the humble bar magnet and ending with a dramatic transformation of the early Universe.
Dramatic transformations
We start our journey with a substance we come across almost every day: ice. Ice is so familiar to us that we just accept the sudden and dramatic metamorphosis of water as it cools below its freezing point. A liquid that we can dive into is spontaneously transformed into a hard rock-like material that would crack our skulls.

Lev Landau
The miraculous transformation that turns liquid water into ice is known to physicists as a phase transition. Many other phase changes are known to physics where, at a well-defined temperature, the structure of a material changes completely. These include the condensation of a gas into liquid, the transformation of liquid helium into a superfluid and the transition of a normal conductor into a superconductor, which happens in a range of materials that lose all electrical resistance at low temperatures.
There are many others. On the face of it, these transformations all appear very different, but in the 1930s the Russian theoretical physicist Lev Landau recognised that they share common features. He realised that in each case, the transformation of the material is accompanied by a loss of symmetry, and this insight was the first step towards building a mathematical model of phase transitions.
Landau's theory represents one of the most important insights in the whole of 20th-century physics. It is remarkable because, as we will see, his reasoning was very general and independent of the details of any particular physical system. For this reason, it applies to a whole range of different areas of physics. There can be few occasions where pure reason has led to so great a pay-off.
Model magnets
To illustrate Landau's theory, imagine a magnetic material, such as iron, nickel and cobalt. These materials undergo a phase transition at a temperature known as the Curie temperature, after the French scientist Pierre Curie, husband of the famous Marie Curie. The Curie temperature of iron is 1043K, which corresponds to 770 degrees Celcius. Above this temperature a lump of iron will lose its magnetism, while below this temperature the iron will spontaneously magnetise.
Landau's theory can be illustrated with a simplified toy model of a magnet. Imagine a collection of atoms arranged regularly in a plane, each atom having a small magnetic field that is constrained to point in one of two directions: it can either point upwards or downwards.

Figure 1: Schematic depiction of the atoms in a ferromagnet. Left: The symmetrical phase above the Curie temperature where all the magnetic fields of the atoms are randomly oriented. Right: The asymmetrical phase below the Curie temperature where the magnetic fields of all the atoms are aligned in the same direction.
According to the laws of thermodynamics, such a system quickly settles in an equilibrium: that's a state of lowest energy. The energy of two neighbouring atoms is lowered slightly if their magnetic fields point in the same direction, so there is a tendency for them to align. However, at high temperatures thermal vibrations vigorously jostle the atoms around with the effect that their magnetic fields are continually being flipped. So, although there might be a tendency for neighbouring atoms to align their magnetic fields, any such alignments are rapidly disrupted. In this state the material will not exhibit a magnetic field macroscopically, as the randomly oriented magnetic fields of all the atoms cancel each other out.
But when the temperature is lowered, thermal vibrations are no longer strong enough to disrupt all of the alignments and most of the magnetic fields will align in the same direction. The material will now have a macroscopic magnetic field. It has become a magnet. As the temperature is lowered further beyond the critical point, the size of the thermal vibrations will decrease to the point where they are so small that even the biggest will not flip atoms into the wrong direction. All the atoms will now be pointing in the same direction.
Broken symmetry gives birth to order
This can be interpreted in terms of symmetry. Above the critical temperature the direction of the magnetic fields of the atoms are arranged completely at random. The magnetic field of each atom is equally likely to be pointing in either direction, so the system does not distinguish between the two directions, they are completely equivalent. In this state the system is symmetrical with respect to the up and down directions. But below the critical temperature this symmetry has disappeared as the magnetic fields of most of the atoms are now pointing in the same direction.
Furthermore, the loss of symmetry below the phase transition is equivalent to a gain in order, as illustrated in this toy model, and this was the key to Landau's analysis. He suggested that there must be a parameter that measures the order. Above the transition temperature this parameter must be zero — as the system is completely disordered and symmetrical. Below the transition temperature the order parameter must take some non-zero value that measures the degree of order that has spontaneously arisen. In the case of a magnet, the order parameter is called the magnetisation. Above the critical temperature the magnetisation is zero, below the critical temperature it is non-zero.
In our simple model the magnetisation $M$ can be defined as $$M=(n_+ - n_-)/(n_+ + n_-),$$ where $n_+$ is the number of the atoms pointing upwards and $n_-$ is the number of atoms pointing downwards. In other words, the magnetisation is equal to the excess of atoms pointing upwards divided by the total number of atoms. Above the critical temperature where magnetic fields are equally likely to point upwards and downwards there is no excess in either direction: the magnetisation is zero, as required. Since it is a physical, measurable quantity it is reasonable to expect that $M$ changes smoothly with temperature. This means that just below the critical temperature the magnetisation should be small, as it is zero just above it, corresponding to a small excess of atoms pointing the wrong way.M and energy
Landau's next step was to write out an expression for the free energy of the system in terms of the magnetisation M. When left alone at a given temperature our system will quickly settle in a thermal equilibrium – that’s the state of lowest energy. However, one can imagine the system being knocked off this equilibrium (while staying at the same temperature) causing the energy to vary briefly before settling back down into equilibrium. Landau wanted to see how this variation depends on magnetisation.
The system is extremely complicated, so it isn't possible to work this dependence out from first principles, there may be all sorts of interactions between the atoms and thermal vibrations that we don't understand. However, Landau realised that close to the critical temperature none of this matters.
To keep things as simple as possible, Landau assumed that the energy $E$ could be represented as a polynomial expansion in $M$. That's an expression of the form $$E(M)= a_0+a_1M+a_2M^2+a_3M^3... .$$ His aim was not to work out the precise value of the energy in terms of $M$ – this would be too ambitious – but to see how $E$ changes with $M$. For that reason, we can ignore the constant term $a_0$ in this expression and only concentrate on those terms that contain a power of $M$. But as it turns out, we can also rule out the linear term $a_1M$ and any terms containing odd powers of $M$, such as $a_3M^3$ or $a_5M^5$. Such an odd power term would imply that a system with, say, $n$ excess atoms pointing upwards has a different energy than a system with $n$ excess atoms pointing downwards. In the first case the excess atoms would give a positive contribution to the energy and in the second they would give a negative contribution and this would contradict the assumption that the two directions are completely equivalent. Therefore, the polynomial can only contain even powers of $M$. Furthermore, all powers of $M$ higher than the fourth power can be disregarded, as they are insignificant close to the critical temperature where $M$ is small. This leaves just two terms in the expansion, terms involving $M^2$ and $M^4$. The result is the following expression for the energy in terms of the magnetisation at temperatures close to the phase transition $$E(M) = a_2 M^2 + a_4 M^4.$$ In keeping with the conventional notation used in this area, we re-write this as $$E(M) = \alpha M^2 + \beta M^4.$$ The question is what the unknown terms $\alpha$ and $\beta$ should be. Landau reasoned that $\beta$ must be positive. A negative $\beta$ would give rise to a graph like the one shown in figure 2. As the graph shows, there would be no minimum energy in this case and this clearly cannot represent a physical system. This implies that there are just two possibilities for the shape of the energy graph.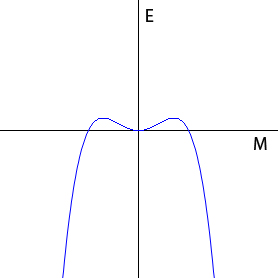
Figure 2: The shape of the graph of E(M) for β negative.
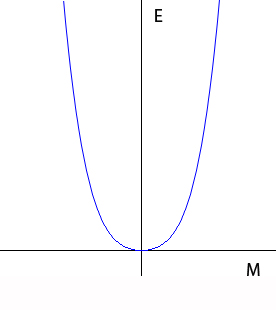
Figure 3: The shape of the graph of E(M) for β and α positive.
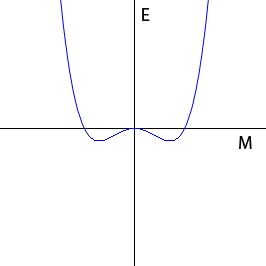
Figure 4: The shape of the graph of E(M) for β positive and α negative.
The mexican hat
Landau's expression relating the energy to the order parameter is applicable to a whole range of phase transitions and the energy graphs generalise in a natural way to higher dimensional systems. For instance, if the magnetic fields were free to point in any direction in a plane rather than being constrained to lie along a single axis, then below the critical temperature the energy graph would look like the illustration below. This is known as a Mexican hat diagram. The energy minima now form a circle within the brim of the hat. At each point on this circle the energy of the magnetic system is as low as possible.
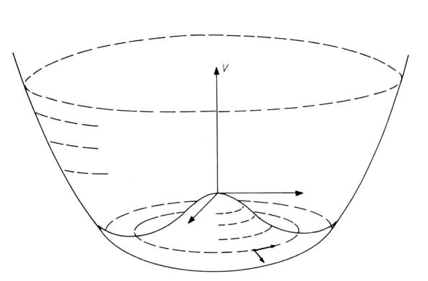
Figure 5: Mexican hat diagram
Landau successfully adapted his theory to the superfluid helium phase transition, work which gained him the 1962 Nobel Prize for Physics, and later, with his colleague Vitaly Ginzburg, to the phase transition of superconductors, once again with great success. It was a combination of the Landau-Ginzburg theory and another superconductor theory developed by John Bardeen, Leon Cooper and Robert Schrieffer that delivered inspiration for the Higgs mechanism (see the book Higgs force for more on this). And it's the Higgs mechanism we will explore in the next article.
About the author

Nicholas Mee studied particle physics and mathematics at the University of Cambridge. He was Senior Wrangler and went on to complete a PhD there with the title Supersymmetric Quantum Mechanics and Geometry. He is the founder of the educational software company Virtual Image.
Mee is the author of the book Higgs force: The symmetry-breaking force that makes the world an interesting place, which has been reviewed in Plus.
Comments
Anonymous
How can this parameter be zero in case when all atoms point upwards or downwards?
M = (n(+) - n(-))/(n(+) + n(-))
It will be either 1 or -1. Am I right?
Marianne
Yes that's right. The magnetisation is zero when atoms are equally likely to point upwards or downwards, ie when there is no excess.