Myths of maths: The golden ratio
This article is based on a talk in an ongoing Gresham College lecture series. You can see a video of the talk below.
Most of you will have heard about the number called the golden ratio. It appears, for example, in the book/film The da Vinci Code and in many articles, books, and school projects, which aim to show how mathematics is important in the real world. It has been described by many authors (including the writer of the da Vinci Code) as the basis of all of the beautiful patterns in nature and it is sometimes referred to as the divine proportion. It is claimed that much of art and architecture contains features in proportions given by the golden ratio. For example it is claimed that both the Parthenon and the pyramids are in this proportion. It has also been claimed that the golden ratio appears in the human body, for example as the ratio of the height of an adult to the height of their navel, or of the length of the forearm to that of the hand.
Yet in my whole career of applying mathematics to the real world I have come across the golden ratio exactly twice. Yes, twice! So are any of these great claims made for the golden ratio true?
What's the golden ratio again?
Let's start by quickly recalling what the golden ratio actually is. It was defined by the ancient Greek mathematician Euclid as follows. Imagine you have a line segment which you would like to divide into two pieces. You'd like to divide it in such a way that the ratio between the whole segment and the longer of the two pieces is the same as the ratio between the longer of the two pieces and the shorter one. What should this ratio be?

We'd like to choose A and B so that (A+B)/A=A/B.
A bit of maths (see here) will reveal that the ratio should be
$$\phi = \frac{1+\sqrt{5}}{2}\approx 1.618.$$The fact that $\phi$ is defined as a ratio between two lengths means that you can look for it whenever you are looking at something that has segments of lines in it - whether that's a face or a building.
The golden ratio in the human body
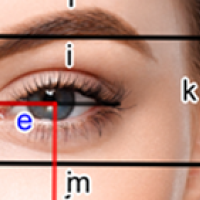
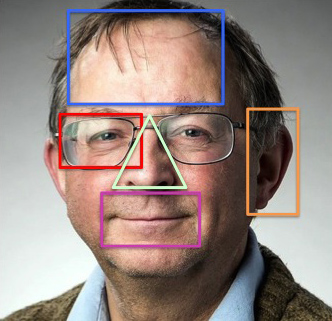
The golden ratio is supposed to be at the heart of many of the proportions in the human body. These include the shape of the perfect face and also the ratio of the height of the navel to the height of the body. Indeed, it is claimed that just about every proportion of the perfect human face has a link to the golden ratio (see this article to find out more about such claims).
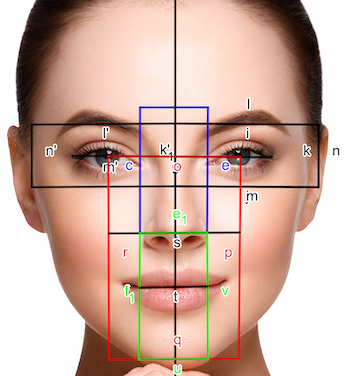
You can superimpose all sorts of rectangles on a beautiful face and then claim that beauty derives from the proportions of the rectangle.
However, none of this is true, not even remotely. The body has many possible ratios, lots of which lie somewhere between 1 and 2. If you consider enough of them then you are bound to get numbers close to the value of the golden ratio (around 1.618). This is especially true if the things that you are measuring are not particularly well-defined (as in the picture on the left) and it is possible to vary the definition in such a way as to get the proportions that you want to find.
If you look hard enough you will also find proportions in the human body close to 1.6, 5/3, 3/2, the square root of 2, 42/26, etc, etc. Indeed most numbers between 1 and 2 will have two parts of the body approximating them in ratio. Similar spurious patterns are also observed in the solar system (which also has lots of different ratios that you can choose from). Also remember that as the golden ratio is an irrational number (see below) you will never see it exactly in any measurement.
All of this is an example of the way that the human brain finds spurious correlations. Indeed given enough data it is possible to find patterns that agree with almost any hypothesis. A good way to see this is to go outside on a nice sunny day and look at the clouds. Sooner or later you will find a cloud, which fits some novel pattern. As an example look at this BBC News article reporting on a "warrior queen" having been observed in a cloud pattern.
This phenomenon can actually be quite dangerous, when spurious correlations are found in data to prove a point. For example they can lead to false accusations and even to false convictions. For a lot of examples of spurious correlations see this website.
Spirals, golden and otherwise
If you take a line divided into two segments $A$ and $B$ so that $A/B$ is the golden ratio, and then form a rectangle with sides $A+B$ and $A$, then this rectangle is called a golden rectangle.
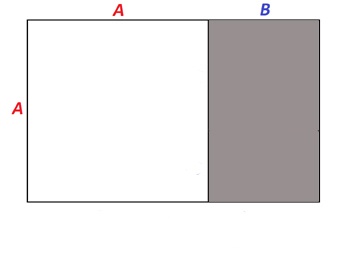
A golden rectangle is made up of a square (white) and a smaller rectangle (grey). The smaller rectangle is also a golden rectangle.
The golden rectangle we have just formed consists of a square and a smaller rectangle, which is itself a golden rectangle (see here to find out more). This golden rectangle again consists of a square and a smaller rectangle, which is itself a golden rectangle. And so on.
Using the sequence of smaller and smaller golden rectangles we can form what looks like a spiral. Simply draw a quarter circle into each of the squares that appear in the golden rectangles.
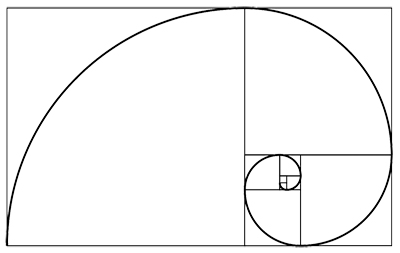
A spiral shape constructed from the golden rectangle.
It is often claimed that this spiral-like shape can be found in many places in in nature and art. For example, as the shape of a nautilus shell, the shape of a galaxy, the shape of a hurricane or even of a wave.
There are two problems here. Firstly, the shape isn't a spiral. It is a sequence of circular arcs. As you go from one arc to another the curvature of the spiral jumps. It is most unlikely that in any natural phenomenon we would see such jumps. In fact, the shape is only an approximation to a true spiral. The form of spiral that it approximates is an example of a logarithmic spiral. Such spirals are very common in nature. They have the polar equation
$$r =a e^{b\theta},$$ where $e$ is the base of the natural logarithm. In nature we see such spirals everywhere, with different values of $a$ and $b$ depending on the context. The reason these spirals are so common is that they have the property of self-similarity. This means that if you rotate the spiral by any fixed angle then you get a spiral which is a rescaling of the original.The so-called golden spiral has the particular value of $b$,
$$b=\frac{\ln{\phi}}{(\pi/2)}=0.3063489...$$ where $\phi$ is the golden ratio (and angles are measured in radians).There is no reason at all why this number is in any way special. The nautilus shell is a logarithmic spiral because the self-similarity property allows the shell to grow without changing shape. The values of $b$ observed for the nautilus shell bear no relation to value above, with the value of $b = 0.18 $ seen most commonly in actual shells.
Art and architecture
We have to be careful here. It is certainly true that some artists, such as le Corbusier (in his Modulor system), have deliberately used the golden ratio in their art work. This is because it has been claimed that the proportions of the golden rectangle are particularly pleasing to the human eye, and that aesthetically we prefer the golden rectangle to all other rectangles. Thus it makes sense to use them in art works. It is then claimed that the golden ratio can be seen in just about every other work of art and architecture.
The evidence for the golden rectangle being especially pleasing is pretty thin. Psychological studies showing different rectangles to groups of people seem to indicate that there was a wide range of preferences, with the ratio of the square root of two to one often being preferred over others. Test yourself on the rectangles below to see which you prefer.

According to Keith Devlin's book Devlin's angle: The myth that won't go away, the idea that the golden ratio has any relationship to aesthetics at all comes primarily from two people, of which one was misquoted, and the other resorted to invention. The misquoted author was Luca Pacioli, who wrote a book called De Divina Proportione back in 1509. The book was named after the golden ratio, but didn't argue for a theory of aesthetics based on the golden ratio, or that it should be applied to art and architecture. Such a view was misattributed to Pacioli in 1799.
Pacioli was close friends with Leonardo da Vinci and it is often claimed that Leonardo himself used the golden ratio in his paintings. There is no direct evidence of this. Perhaps the most famous of these examples is the Vitruvian Man. However the proportions in this painting do not match the golden ratio. Indeed Leonardo only mentioned whole number ratios in his works. Supposed examples of the golden ratio appearing in his pictures are in the same class as those finding the ratio in nature.
Devlin attributes the "popularisation" of the golden ratio to Adolf Zeising, a 19th century German psychologist who argued that the golden ratio was a universal law that described "beauty and completeness in the realms of both nature and art [...] which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical." This was simply an example (as above) of seeing spurious patterns. However, Zeising's work went on to influence many others, and laid the foundations for much of the modern myth.

The so-called golden spiral superimposed on the Parthenon. There is no evidence that the golden ratio played a role in the design of this building. Underlying image of the Parthenon: Oyvind Solstad, CC BY 2.0.
Another example of this myth is the claim that the golden ratio appears in the proportions of the Parthenon, part of the Acropolis in Athens.
There is no evidence of this in Greek scholarship, and the idea that the Parthenon has proportions given by the golden ratio only dates back to the 1850s. Furthermore, the actual measurements of the Parthenon do not give proportions especially close to the golden ratio, unless you are careful with your choice of rectangles. In fact, the Parthenon takes its harmonious appearance from the clever deployment of lines that look parallel but in fact converge or curve, so it's virtually impossible to take measurements precise enough to give exact ratios. As the proportions of the Parthenon vary with its height it is simply not possible to find an overall proportion that agrees with the golden ratio.
The same applies to the rest of Greek architecture: there is no evidence whatsoever that the Greeks considered the golden ratio aesthetically pleasing, or used it in their art and architecture at all.
It also applies to music. It is claimed that the golden ratio is important in musical composition. There is little evidence of this. However what is important in composition is the scale, and the scale is very closely linked to the twelfth root of 2. It is this latter number which lies at the heart of music, not the golden ratio [reference}.
There is very real danger in these persistent myths about the golden ratio. School children and many others are being duped into a false reality about the way that maths works. Sooner or later they will find that this reality is untrue, and will lose faith in the very real ability of maths to explain the world.
The great reality
Having been rather dismissive about the golden ratio I would like to conclude this section by stressing just how amazing a number the golden ratio really is - it really doesn't need all those spurious claims to make it special.
First, let's turn to natural phenomena that really are related to the golden ratio. The golden ratio is intimately related to the famous Fibonacci sequence
$$1,1,2,3,5,8,13,21,...$$You can find out more about this link here. The Fibonacci sequence certainly does appear in nature as it is both linked to the way that populations grow, and also to the way that shapes can be fitted together. For example, the sequence can be seen in the spirals on sun flowers which have to fit together in an ordered fashion, and in the leaves on some plants that need to be arranged to capture the most sunlight. As a result it is possible to observe ratios close to the golden ratio arising in certain natural phenomena (find out more here).
These phenomena include the distribution of drones to female bees in a bee-hive, which is linked to the way that bees reproduce over many generations (find out more here). So it is indeed possible to see the golden ratio in the garden, and there are very good mathematical reasons for this.

Fibonacci thought of his sequence when considering the population growth of idealised rabbits. See this article to find out more.
But perhaps even more interesting are the many fascinating mathematical properties of the golden ratio. These are explored in various Plus articles, but I would like to point out one that is particularly fascinating and which really sets the golden ratio apart from other numbers: its extreme irrationality.
Irrational numbers are numbers that can't be represented by fractions and that have an infinite decimal expansion that doesn't end in a repeating block. This very fact means that it is hard to observe irrational numbers in nature. The golden ratio has the amazing property of being the most irrational number of them all. This means that not only is it not possible to represent it exactly as a fraction, it isn't even possible to approximate it easily by a fraction. See this article for the mathematical details.
The difficulty of approximating the golden ratio by a fraction makes it a very useful number to mathematicians and scientists studying the process of synchronisation. This occurs when a system with a natural frequency is forced by one of a different frequency, and adopts the forcing frequency. One example is the synchronisation of the human body to the daily frequency of sunlight. A second example is the Earth's climate which synchronises to the natural cycles of the orbit around the Sun.
However, synchronisation can itself be a problem, leading to unwanted resonances in a system (such as a suspension bridge vibrating severely if a marching band walks over it). By choosing two frequencies in the ratio of $1:\phi we can avoid synchronisation due to the extreme irrationality of the golden ratio. This very useful property appears to be exploited by the brain and insect species as well as climate scientists and even people who manufacture aircraft.
So the golden ratio does have a starring role, but not one that you often read about in the mythology associated with it. This is a great pity! It is a lovely paradox that the most interesting thing about the golden ratio is that it isn't a ratio.
About the author
Chris Budd.
This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.
Comments
Mauro
The claim about the golden ratio in music actually refers to form, not to frequency (though that doesn't stop people from making music with tunings related to the golden ratio, but anyway). The claim is that if you have some work with an AB form, the A and B sections will ideally have durations in the golden ratio, etc., because the golden ratio provides the best balance between durations or something. I think it's claimed that this proportion can be specifically found in the music of Mozart.
While we're at it, 2^(1/12) isn't particularly special either; it's mostly a coincidence and a compromise. "Ideal" frequency ratios are in small whole numbers, but these come with some mathematical challenges (like the fact that (3/2)^4 ≠ 5) and it was generally decided to settle on a compromise system with 12 equal steps to the octave rather than unequal steps with "nicer" numbers or, say, a different number of equal steps (like 19 or 31).
Manjunath Mahashetti
Golden Ratio is widely practised in the variois drum beats in Carnatic music. They follow rule called 'Hemachandra series - about 100byears prior to Fibonacci himself'. Also see Melakarta rules structure in Carnatic music. Would love to having a discussion on it
rasamaya
The smaller part goes into the larger as the larger goes into the whole. So the small portion is a ratio of the larger Portion in the same ratio that the larger portion goes into a whole.
how is this not a ratio?
Marianne
The statement refers to the fact that phi is irrational, hence not a ratio between two integers.
Raúl A. Simón Eléxpuru
Great article that exposes the whole "golden ratio" baloney! One comment, though: you cannot say "degrees are measured in radians", as in the next-to-last paragraph of the section titled "Spirals, Golden and Otherwise"; it is like saying "meters are measured in feet".
Marianne
Very true, thanks for pointing that out. We have corrected it.
jbmacp
Note that in Lego bricks the golden ratio is to be found in several aspects, including the relationship of the studs and tubes. It has been claimed as a significant contributor to their commercial success, although it may be that the system was in part inspired by Le Corbusier architectural designs
Jayadeep
Can't we use 2 consecutive Fibonacci numbers(in the higher range) to approximate the golden ratio ?
Chris Budd
Yes you can, and in fact these are the best rational approximations to the golden ratio. However, they are still poor approximations and even if you take numbers in the higher range the approximation is not good, and only slowly converges to the correct value. This is in contrast to a transcendental number such as pi which you can approximate much better by using a fraction. For example the approximation of pi given by 355/113 is very good indeed, and much much better than you would get for phi for the ratio of two succesive numbers in the Fibonacci sequence such as 233/144.
R. Mashlan
Yes you can. This is because any linear recurrent sequence such as the Fibonacci sequence approaches proportionality to the Golden Ratio raised to the nth power for the nth term (see Binet's formula for generalized linear recurrent sequences). This was conjectured by Johannes Kepler in Harmonics Mundi, published in 1619, and even earlier by a lesser known German mathematician Simon Jacobs.
PatronDemon
You assume the golden ratio is strictly limited to exact formations.... Its not and no one ever claimed it was.
The fact that you took the generalization that holds try when averaged then complained about individual examples not matching it perfectly shows a gross lack of understanding of the mathematical applications.
You are looking at a scatter graph complaining 8ts not linear.
Explain to me then why life conforms to the golden ratio? Why do flowers have 3 or 5 petal increments? Ratio x2 rounded or x4 rounded.
You ignore that this is a living number and that life rounds things as you cant have a partial petal or head as a standard.
Your pantheon example somehow measures the front? When the golden ratio is applied to the base....
The greatest issue is you clearly think that math is hard unflinching fact. No. Math is our description of the world. For example if i say no tree is taller than ten increments in height. Then we defining that increment does not change the height of the trees.
Additionally.... And most horrifying of all... You are using an incorrect equation to calculate the golden ratio. 1+root 5 over 2? No ...
Golden ratio is a mathematical feed back loop. X= 1+1/x.
So 1+1/(1+1/[1+1/{1+1/<1+1/...>}])....
When your equation is flawed and you are attempting to force it to work perfectly in a science that is widely recognized as variable aka soft science. And relies on generalization and not unbendable law.
You also face the issue that your convinced somehow that the ratio is a two dimensional rectangle being applied to three dimensional shapes....
Perhaps measure the branches of a tree and watch the ratio define how the branches split?
I have. Its accurate 75% of the time. When you apply mathematics to soft sciences that vary aka anything that is being used to measure living things. 75%-80% is enough to state a rule.
Your argument quite bluntly disproves all medical sciences because no two people have identical hearts and since its not identical mathematically it must mean the theory behind heart disease is wrong because EVERY heart is not identical.
To disprove a theory such as this you cannot disprove it as you have. That's not how science works. You have to attempt to prove it and find what breaks it so completely that is disproven. Please site an example that none of them matched (not just a majority). You seem to have made many test but refuse to examine the averages that fall almost exactly on the ratio.
No ones ratio will be exactly 1.6... But the more times you test it the closer to 1.6 it becomes. The golden ratio is not an exact answer. But put your results through calculus graphing. You'll find like limits, the more samples you take the closer to the limit 1.6 your graph will get.
Examining individual samples and not as a whole is not how you do math or science.
You have not disproven or even dented the golden ratio argument. You have only argued variable facts that supporters of the golden ratio theories have already successfully explained the apparent discrepancies of.
If you simply ignore the fact that math is the measurement of patterns in nature and that the golden ratio is the continuously occuring pattern in life... You did not disprove the golden ratio, you disproved math and science.
When math disproves itself it typically means the person was wrong as math cannot disprove itself by its nature. I believe that your mis-printing of the ratio fraction is the primary cause. Your equation is basically converting pi to 3.14 before calculations. That kind of early conversion of a fixed number causes massive discrepancies in your math. By not converting my ratios, my equations always had a smaller +- variable than my professor in calculus. I assume you expecting exacting answers in a soft science, refusing to view all of your result objectively (via scatter plot or averages) led to this extreme inconsistencies in your attempted disprovable of this theory.
The nature of life is its an approximation, a rounding of a universal equation we have not unlocked. But the golden ratio is ultimately part of it as the golden ratio is the closest number we can get to infinite.
Laszlo
Just a quick reminder: you absolutly can calculate the ratio by 1 + sqrt(2) / 5 just as well as with your "feed back loop". Two methods for the same results.
Source:
https://en.wikipedia.org/wiki/Golden_ratio
Here your "feed back loop" formula is shown under the section "continued form" and the square root formula is shown under the "algebraic form" section.
BTW, fun fact: How much decimals of PI does NASA use for their highest precision orbital calculations? 10,000? 5,000? 1,000?
Just 15! For the Voyager spacecraft this imprecision equates with an error of its position of only 1.5 inches after travelling more than 12.5 billion miles.
Source: https://www.jpl.nasa.gov/edu/news/2016/3/16/how-many-decimals-of-pi-do-…
Karl Lew
PatronDemon, having read the Wikipedia article on the Golden Ratio, I do require now some proof of your horror. The Wikipedia article derives the Golden Ratio from the quadratic solution for x^2 - x -1 = 0 per the definition of self-similarity of line segment ratios. That is also the definition and derivation quoted by the author. The Wikipedia article also lists your continued fraction as an alternate formulation for the same number. Where's the horror?
skothr
[I just realized my response had a random link, so it may have been filtered. This is a direct copy without the link.]
I agree with some of your points at a high level, but at the very least they do have the equation correct. It's not an approximation -- the irrationality is derived from the square root of 5. I was caught off guard myself when I first saw such a simply-defined expression being equated to phi.
But the math works out to the same expression you provided.
Let x = (1 + sqrt(5)) / 2
Prove:
x = 1 + 1 / x
Calculate 1/x:
1/x
= 1 / ((1 + sqrt(5)) / 2)
= 2 / (1 + sqrt(5)) : [1/(a/b) = b/a]
= 2*(1 - sqrt(5)) / (1 - 5) : [multiply by (1 - sqrt(5))/(1 - sqrt(5))]
= 2*(1 - sqrt(5)) / (-4) : [simplify denominator by addition]
= (1 - sqrt(5)) / (-2) : [cancel out factor of 2]
= (sqrt(5) - 1) / 2 : [bring negative sign up to the numerator]
That's 1/x, so now add 1 to get (1 + 1/x):
1+1/x
= 2/2 + (sqrt(5) - 1) / 2 : [2/2 = 1 and 1/x = (sqrt(5) - 1) / 2]
= (2 + sqrt(5) - 1) / 2 : [combine fractions with same denominator]
= (1 + sqrt(5)) / 2 : [combine terms in numerator, 2 - 1 = 1]
= x
Thus, x = 1 + 1/x if x = (1+sqrt(5))/2
ΟΕΔ
Personally, the significance of the square root of 5 reminds me of the dodecahedron (made of pentagons) which Plato thought to represent the cosmos.
Khoa
Wow, thank you so much. Somehow you manage to help me understanding a lot more about statistic and how math should be applied in soft science. I'm not an expert on the field though, so I can only give you this message as appreciation for taking time to explain this throughly. I also understand more why calculus is so important in finding the limit, something which evade me for 2 years of watching youtube video on the subject.
Jesús
1.- 820/261 = 3.14176 (numérica)
2.- (1+ 1/5) * (Phi)^2 = 3.141641 (geométrica)
David Gallagher
Chris, I was doing my due diligence for a project I wanted to do concerning the golden ratio and wanted to provide an example of the golden ratio (or golden spiral) in nature and web page after page gave me "examples" of what I thought I was looking for. Upon closer inspection, it seemed wild conjecture that the spiral used was a golden spiral and was in reality, I thought, just a logarithmic spiral of which there can be many types. I also saw many works of art with golden rectangles all over them showing positions of features. Seeing these, I thought I could take any photo or work of art and go golden rectangle hunting to find these relationships among the features. I thought the whole thing a scam or I was missing some point until I saw your article that expressed my state of mind perfectly.
I do like your inclusive of the fact that the golden ratio does not need any embellishment. I do think the ratio to be pleasing and have included in some furniture designs I have done but understand that this choice might not be the most appealing to all. When faced with design choices on placement, considering golden ratio relationships is not a bad place to start.
E X Stoat
+1 Well put.
As an architecture student in the 70's-80's I desperately wanted to find proof that modernism
was not simply a "stylistic expression of a particular philosophy"
Studying Corbu's Modulor on my own, I realized that, while a great architect, logical argument was not his forte... I still have the metal stencils of his alphabet someplace.
R. Mashlan
I believe that your article is based on Dr. Murkowsky's 1992 article, "Misconceptions about the Golden Ratio", which like your article, is dismissive of applications of the Golden Ratio to art in architecture in western culture starting with Classical Greece. Devlin, who often quotes Murkowsky's article, seems to attribute the "popularization" of the Golden Ratio to the minor character Adolf Zeising.
I believe this dismissive arguments are in error. First, artists and architects are not usually in the habit of explicitly documenting their reasoning behind their creative decisions and leaving behind such written evidence for historians. Secondly, during the European Renaissance, Euclid's Elements was the foundational textbook on geometry and mathematics. This textbook has no less than ten references to the "Extreme and Mean Ratio", and any student of geometry learning from this text would have had to work through the several propositions that required the Golden Ratio.
Euclid's Elements was required study in European universities up until the mid 20th century, and it would be hard to explain why the "Extreme and Mean Ratio" would not have an undue influence on western art and architecture, since I imagine these learned artists and architects of the past all having a copy of this textbook on their bookshelves.
The Parthenon, built only two centuries before Euclid of Alexandria summarized ancient Greek knowledge of geometry in Elements, does have elements of the Golden Ratio in its design, the most obvious are within inscribed artwork within the upper facade, where many golden rectangles are found. Murkowsky's dismissal of the front of the Parthenon having Golden Ratio proportions have to do with the convenient subtraction of the stylobate (the base foundation and the series of steps of that lead to the level where the columns are placed), and he makes no further investigation into application of the Golden Ratio in the Parthenon's architecture. This dismissal has been repeated by Devlin and Livio and others, and is unfortunate, as it is reaching mythical proportions.
The Golden Ratio has been found throughout Renaissance art and architecture and beyond. For instance, consider the Pyramide du Louvre, which was constructed at the entrance to the Louvre Museum in Paris, and was designed by 20th century chinese-american architect I.M. Pei. Pei has stated that the design of this pyramid was not based on dimensions of the Great Pyramids of Egypt, but instead on the Golden Ratio.
Finally, I present for consideration the architecture and street layout of Washington, D.C., the early 19th century preplanned city which is the capital of the United States of which there are many obvious manifestations of the Golden Ratio. Although the design decisions were not explicitly documented, it may be deduced that since many of the founding fathers of the United States were freemasons, a secret society originating in Renaissance stonemason guilds, inclusion of this "sacred geometry" is not to be unexpected.
Rick
The golden ratio also shows up when solving the ancient geometric problem of squaring the circle using the yin yang method. Which I believe is the minimum amount of steps you can use to "solve" the problem. Interestingly, the circle represents the spirit, or metaphysical, and the square represents the physical world we live in and Phi is in between them. The square, which is the most basic 2 dimensional shape possible, represents this plane we live on and the circle, a 1 dimensional shape represents the spirit, Phi, which looks like a vibrating string in the solution is the beauty that bridges the two
sneed
I'm a freshman in college and learning about the golden ration was interesting, but at the same time I questioned a lot of the claims about it being aesthetically pleasing and such (which led me to find this article), knew I wasnt the only one who thought of that before
Cool article