Maths in a minute: Social distancing
Imagine lots of people in a park, sitting in the Sun. Each person wants to keep at least 2m distance to everyone else, but they want to have as many people as possible at the minimum 2m distance. How should the people arrange themselves to make this happen? And what's the number of people a person will have exactly 2m away from themselves in this arrangement?
See here for all our coverage of the COVID-19 pandemic.
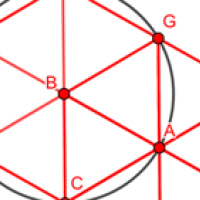
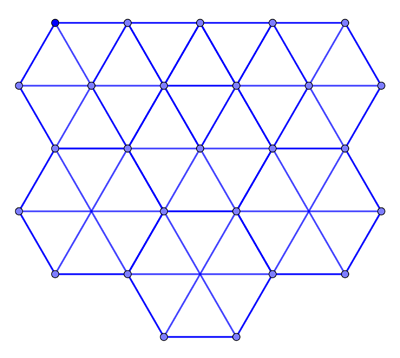
Let's start with a single person whom we will call person A. People who want to be 2m away from person A should position themselves somewhere on the circle that has A as its centre and a radius of 2. Let's look at two people on this circle, B and C. Since B and C also want to be 2m away from each other, the triangle formed by A, B and C should be an equilateral triangle with side length 2.
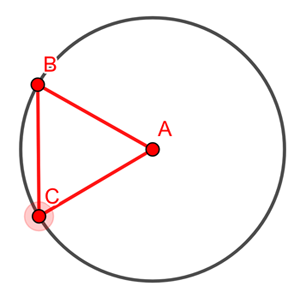
How many such triangles can you fit around A so that they don't overlap? Well, the angles in an equilateral triangle are all 60 degrees. There are a total of 360 degrees available around A, which means that you can fit exactly 360/60=6 equilateral triangle around A. In other words, the number of people that can position themselves 2m away from A and also be 2m from each of their two neighbours on the circle is six.
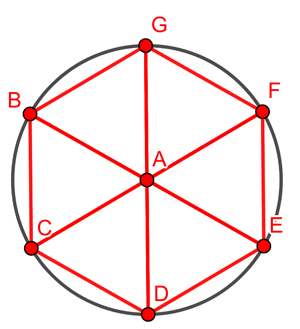
Now exactly the same argument holds for any other person on A's circle. The number of its closest neighbours, exactly 2m away is six, and they should be positioned around the person in the shape of a regular hexagon made up of six equilateral triangles.
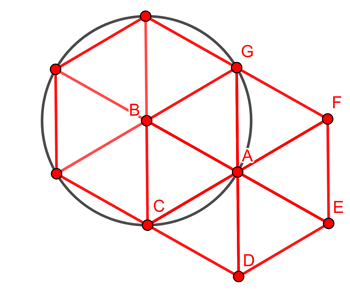
Since this works for every person the answer is that people should arrange themselves on a triangular lattice made up of equilateral triangles. Every person in the lattice is also at the centre of a regular hexagon.
Comments
Terence Mills
I infer from this article that a safe distance in the UK is 2m; in Australia it is 1.5m; in Singapore it is 1m. Where do these numbers come from?
Evie Winters
Well, all those distances are what’s considered okay in those specific countries. I live in America, where we don’t really use metres, and we stay 6 feet apart, or roughly two metres. It’s only because that’s what the government of that country thinks is safe.
Anthony
This works when everything is static, but only those on the perimeter can leave. I wonder what the densest configuration would look like where anyone can leave while still maintaining a minimum distance from all others.
Martin Douglas
Purely from the visual above I'd say take out every 3rd diagonal, like // // //, and there'd be a corridor for movement from either side, always 2m. Sorry, can't do the maths.
python
great post . but it is not realistic as it is not time varying .And doesn’t count physical obstruction such as building, road ect…. can you include this factors and post more realistic model for social distancing .thanks.
Paul Prebble
It's all very well having a 2m lattice but shouldn't it also ensure that the people's heads are on the vertices and how people would get to and from their spot? The latter would reduce the total number by a third.
Soh
In a 4x4 square, you can position 9 people at least 2m apart, but if we adopt this arrangement of equilateral triangles, you get only 8. Right!
shane lilly
a 4x4 square takes up 16 square meters of area where as the hexagon with 7 people takes up less area. 10.4 square meters.
comparing space per person that would be 1.77 square meters per person for the square vs 1.48 square meters for the hexagon.
Mark99504
Got a 4x4 area, your arrangement fits 9, while triangles fit 8. Got an 8x8 area, squares fits 25, triangles fits 24. Got 12x12? squares 49, triangles 50. 16x16? squares 81, triangles 91 (I think).
Each time you add more people past 9 or 8, you have to position them far enough away from everybody else. As the number of people increases, triangles take less area to achieve adequate distance for each person.
Math Teacher
Yes, but in a 7x7 square, triangles allows for 20 people, while squares only allow for 16.
RichCatt
A 4x4 square can take 9 people in an area of 16 sq. m, and the triangles can take 10 people in an area of 17.32 (10 x sqrt 3) sq. m, so the comparison depends on the shape we are trying to fill.
Kittwit
In the given scenario of a large park with no discernable edges this solution would be efficient. The problems start to occur in smaller spaces when boundaries such as walls are present. In these situations there would be a lot of space lost at the edges with hexagonal packing and the conventional square packing is often more efficient. The edge effect becomes less of an issue above about 50 individuals though as the lost space becomes relatively less. So in a wide space with more than 50 people use hexagonal packing. If you're in a room a square arrangement is probably better.
John Franklin
actually, in a 4x4 square not everyone is 2m apart. the person in the middle is <2m from those on the corners, I believe they are sqrt2 meters away.
Nontokozo Mkhwamubi
Hi I would like know how did you figure out 9, which method or approach did you use?
Willy
Fascinating.