The Sun, the Moon and trigonometry

How much further away is the Sun than the Moon? How much bigger is the Sun than the Moon? And how are you supposed to work out the answers if you are an ancient Greek who doesn't even have a telescope?

If you are Aristarchus of Samos, who lived around 2300 years ago, then you'll rely on your excellent geometrical expertise combined with an important insight: that the Moon shines at night because it is illuminated by the Sun. On the face of it, this latter fact is far from obvious, but then Aristarchus was a pioneer. Unlike many, many astronomers who came after him, he recognised that the Earth moved around the Sun, rather than the other way around.

Armed with the knowledge that the Sun illuminates the Moon, Aristarchus realised that at half Moon, the triangle formed by the Earth (E), the Moon (M) and the Sun (S) has a right angle at M.

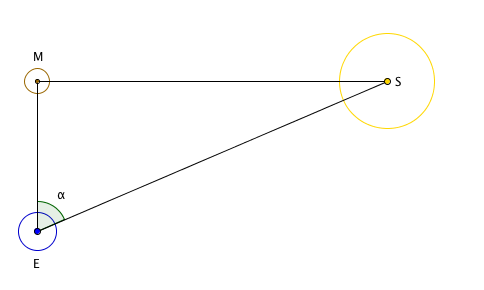
Diagram not to scale.

You can convince yourself of this by imagining the Sun in different places in the diagram above and checking that the parallel rays of light emanating from it illuminate exactly half of the Moon (as seen from Earth) only when there is a right angle at M.

Aristarchus was after the relative distance to the Sun and the Moon, that is, he was after the ratio $\frac{ES}{EM},$ , where $ES$ is the distance from the Earth to the Sun and $EM$ is the distance from the Earth to the Moon. If you know your trigonometry you know that

$\frac{EM}{ES} = \cos {\alpha },$

where $\alpha$ is the angle at the corner $E$ of the triangle. Therefore

$\frac{ES}{EM} = \frac{1}{\cos {\alpha }}.$

Taking the estimate $\alpha = 89.85^\circ$ gives the answer

$\frac{ES}{EM} = \frac{1}{\cos {89.85^\circ }} \approx 382.$

So the Sun is just short of 400 times further from Earth than the Moon. Aristarchus also noticed that during a solar eclipse the Moon completely covers the Sun. This gives us the following diagram: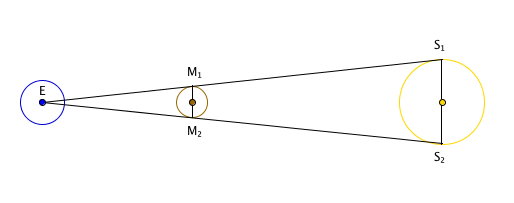

Diagram not to scale.

Using the fact that the ratio between $ES_1$ and $EM_1$ is the same as the ratio between $S_1S_2$ and $M_1M_2$ (because we are looking at two similar triangles) we can deduce that the Sun’s diameter is about 400 times bigger than the Moon’s diameter.

The result Aristarchus came up with was very different. He estimated the Sun to be between 18 and 20 times further away than the Moon. This is partly because he didn’t have the means to measure $\alpha$ accurately enough and took it to be equal to $87^\circ .$ Using this value in the calculation above gives that the Sun is about 19 times further away than the Moon: a small variation in an angle $\alpha$ close to $90^\circ$ leads to a large variation in $\frac{1}{\cos {\alpha }}$ .

The reason why Aristarchus could only come up with the range from 18 to 20, rather than a single number, is that trigonometry hadn’t been developed yet. He didn’t have the notion of a cosine, let alone any tables in which to look up the cosine of a given angle. Instead, he had to use a more complicated geometric argument to come up with his approximate answer. Which illustrates why trigonometry is so useful for astronomers.

About the author

Marianne Freiberger is Editor of Plus.

Comments

Please can you explain why

Please can you explain why you would estimate alpha to be almost 90 degrees? The angle at corner M is 90 degrees but the angle at corner E is much closer to 60 degrees.

The diagram is not drawn to

The diagram is not drawn to scale, which is why the angle alpha in it doesn't reflect the angle you would observe in reality.

how can we know it is 89.5

i mean how could we know it is 89.5? please explain the way to find 89.5

The value 89.5 degrees comes

The value 89.5 degrees comes from observation.

How to know the angle is 90 degrees

Hello! Are you familiar with the Unit Circle? The unit circle is like the lifeblood of trigonometry. Look up an image right now. Learn about it. If you look at the circle E and notice the location of the line EM as it intercepts the circle E, and then you compare it to the unit circle, you will notice that the line intercepts at the location ~90 degrees on the unit circle (or pi/2 in radians).

That might not make sense right away, but study the unit circle and you'll get it!!

Good luck!!

Hope that helps!

how can we know it is 89.5

Since the sun is very far away, the rays from the sun will be almost parallel to both the earth and the sun. So this means the angle of rays between the sun and the moon will be very small. Given the moon is perpendicular to the earth, we have 90 deg on that angle. Since the angles of a triangle add up to 180 deg, the remaining angle is very close to 90 deg, so 89.5 is a good approximation. (It could be 89.8 or 89.7) The result will be similar.

89.5 is not a good approximation if it really was 89.8 degrees.

In angles very close to 90 degrees, a small error can make a very large difference. If the angle was really 89.8 degrees, the result would be very far from the result with 89.5 degrees.

Maths

Triangle of sun and moon and earth

Studying

Since we have assumed that it is a situation at night thus the sun from you (observer) is very far away as compared to the moon (at night). Now about the angle -->
Angle M=90
Angle ESM is the angle of elevation of the sun from earth and as already stated that sun is very far away thus angle of elevation is very less. Thus angle MES (α) is assumed to be 89.5