
Outer space: Where to stand to look at statues

The Sphinx, at Giza (Image by Usuario:Barcex CC-BY-SA-3.0)
Many of the great cities of the world offer fine statues to be admired from a distance. Usually, they stand on pedestals or are affixed to facades far above our heads. Where should we stand to get the best possible view of them? If we stand very close we find ourselves looking almost vertically upwards and capture only a small cross-section of the front. So we need to be further away, but how much further? As we go away from the statue on its pedestal it appears smaller and smaller; closer and it looks steadily larger until we get too close and it starts to look smaller again. In between there must be an optimal viewing distance, in the sense that the statue appears at its biggest.
We can find this distance by setting up the viewing scenario as in the figure below. You, or rather your eyes, are located at $Y$; the height of the statue’s pedestal is $T$ above your eyes and the height of the statue on top of it is $S$. These distances are fixed but we can change $x$, the distance you stand from the pillar.
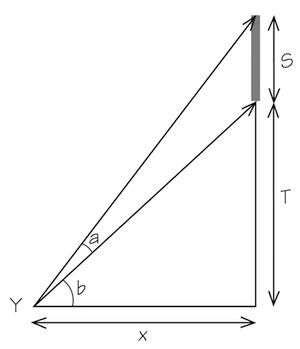
A little geometry helps. The tangents of the angles $b$ and $b + a$ between the ground and the top of the pillar and the ground and the top of the statue, respectively, are given by: $$ \tan(a+b) = \frac{(S+T)}{x} \mbox{ and } \tan(b) = \frac{T}{x} $$ If we use the formula for: $$ \tan(a+b) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)} $$ then we find that: $$ \tan(a) = \frac{Sx}{x^2 + T(S+T)} $$ Now we want to find the value of $x$ for which the angle $a$ spanning the height of the statue is maximised. To do this we just work out the differential $\frac{da}{dx}$ and set it equal to zero. (This differential is the rate of change of the angle $a$ with the distance from the statue $x$. You can find out more about calculating these in Making the grade.) Differentiating, we have: $$ \sec^2(a)\frac{da}{dx} = \frac{-S(x^2 - T(S+T))}{(x^2 + T(S+T))^2} $$ Since $\sec^2(a)$ is a square it is positive for a values in between 0 and 90 degrees; we see that $\frac{da}{dx} = 0$ and the statue looks biggest when the numerator on the right-hand side is zero – that is, when: $$ x^2 = T(S+T) $$

Nelson on his column (Image by Eluveitie CC-BY-SA-3.0)
This is the answer to our question. The optimal viewing distance $x$ that makes the facade of the statue look the largest is given by the geometric mean of the altitude of the pedestal and the altitude of the top of the statue, or $x = \sqrt{T(S+T)}$.
We can try this formula out for some well-known monuments (we'll assume that a person's eyeline is 1.5m above the base of the pedestal in these examples). Nelson’s Column in Trafalgar Square in London has $T = 50$m above eye level, roughly, with $S = 5.5$m so you should stand about $x = \sqrt 2775 = 52.7$m away to get the best view. The Sphinx, at Giza just south of the Pyramid of Khafre, has $S = 20$m and $T = 43.5$m so the optimal viewing distance is at 52.6m. Michelangelo’s statue of David in Florence has $S = 5.17$m and $S + T = 6.17$m so we need step back only to $x = 2.48$m for the best view. If you want to prepare for your visit to view one of the world’s great statues on a pedestal then you can find the dimensions you need for calculating the optimal viewing point on helpful websites.
About the author
John D. Barrow is Professor of Mathematical Sciences at the University of Cambridge, author of many popular science books and director of the Millennium Mathematics Project of which Plus is a part.
This article is an extract from Barrow's new book 100 essential things you didn't know you didn't know about maths and the arts. You can hear John talk about his new book, and help him celebrate its launch with a drink after, at 6pm on Thursday 13 November at Gresham College. See their website for more information.
Comments
Anonymous
Given the answer has a very simple form, perhaps there is another way to develop the result using elementary (non-calculus) method ?
David Pavett
Yes there is an easier non-calculus method for obtaining the same result. It is based on the idea the three points define a unique circle. The three points are the top of the statue (A), the bottom of the statue (B) and the eye(s) of the observer (C). This circle is minimised, giving the best viewing angle when the horizontal line through C is tangential to the circle. This is easy to see when the diagram is draw. A few simple construction lines the set up two similar triangles from which the result is directly obtained.
Anonymous
Consider a slightly more general situation, where the line segment S of the statue is being viewed from a point on a line V positioned generally (rather than a line perpendicular to the line segment as given in the problem). To determine the best vantage point on V from which to view S, note that if the circle determined by the end-points of the segment S and the current vantage point is such that the line V moves cuts the circle, then any point on the corresponding chord will have a larger viewing angle (follows readily using the constancy of angles at the circumference standing on a given chord, S in this case). Therefore, at the best viewing point, the circle must be tangent to V.
In the given case, where V is perpendicular to S (extended), the distance of the viewer to S extended can be shown by elementary means to be given by the formula above.
Anonymous
In fact Holmes, the circle with the chord S and tangent to line V has its center equidistant from the endpoints of the segment and from the line. Thus the center is on the locus of points equidistant from the line V and one of the endpoints of S (either will do), that is, on the parabola with focus the endpoint and directrix V.
Anonymous
Holmes and Watson were sitting quietly, awaiting the arrival of the guest for the New Year's Eve dinner Holmes had arranged. "In fact, Watson,", Holmes observed, "even more elementarily than your parabola, the circle with centre the point R of intersection of line V and the segment S extended and passing through the optimal vantage point has radius given by the same formula in T and S, provided T is interpreted as the distance from R to the segment S. This can be shown by using Pythagoras's Theorem twice." At that moment the door chime sounded. "That must be Miss Adler. I look forward to her telling us the latest from Paris and her discussions with Poincare. You may not be aware that she and he were both students at the same time of Hermite."
Anonymous
Is it the fact that if the statue stands exactly on the eyesight level, i.e., T=0, then we should go as close as possible to it?