
Too big to write but not too big for Graham
Recently, when we were writing our book Numericon, we came across what has now become one of our very favourite numbers: Graham's number. One of the reasons we love it is that this number is big. Actually, that's an understatement. Graham's number is mind-bendingly huge.

The observable Universe is big, but Graham's number is bigger. Image: ESA and the Planck Collaboration.
Our new favourite number is bigger than the age of the Universe, whether measured in years (approximately 14 billion years) or seconds (4.343x1017 seconds). It's bigger than Avogadro's number, a sizeable 6.02214129 x 1023. This is the number of hydrogen atoms in 1 gram of hydrogen, which is called a mole and is the standard unit for measuring an amount of a substance in chemistry or physics.
Graham's number is bigger the number of atoms in the observable Universe, which is thought to be between 1078 and 1082. It's bigger than the 48th Mersenne prime,
257,885,161-1,
the biggest prime number we know, which has an impressive 17,425,170 digits. And it's bigger than the famous googol, 10100 (a 1 followed by 100 zeroes), which was defined in 1929 by American mathematician Edward Kasner and named by his nine-year-old nephew, Milton Sirotta. (This might sound familiar, as Google was named after this number, though they got the spelling wrong.)
Graham's number is also bigger than a googolplex, which Milton initially defined as a 1, followed by writing zeroes until you get tired, but is now commonly accepted to be 10googol=10(10100). A googleplex is significantly larger than the 48th Mersenne prime. You, or rather a computer, can write out the 48th Mersenne prime in its entirety, all 17,425,170 digits of it. But, despite the fact that I can tell you what any digit in the googolplex is (the first is a 1, the rest are all 0), no person, no computer, no civilisation will ever be able to write it out in full. This is because there is not enough room in the Universe to write down all googol+1 digits of a googolplex. As Kasner, and his colleague James Newman, said of the googolplex (in their wonderful 1940s book Mathematics and the imagination which introduced the world to these numbers): "You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way."
Graham's number is bigger than the googolplex. It's so big, the Universe does not contain enough stuff on which to write its digits: it's literally too big to write. But this number is finite, it's also an whole number, and despite it being so mind-bogglingly huge we know it is divisible by 3 and ends in a 7.
A big party
The origins of Graham's number go back to 1928 when a brilliant young mathematician, Frank Ramsey, noticed a surprising thing when he was working on a paper about logic: complete disorder seemed to be impossible. No matter how complicated your system looks, pockets of order of any size are always guaranteed to be there if the system is large enough.
This result, which was just a small part of the particular paper he was working on, was the start of a whole new field of mathematics called Ramsey Theory. This area of maths is often explained with the example of a party. Suppose you're having a party and you want to make sure you invite a good mix of people and decide to keep track of who knows who. Suppose you draw a map of the relationships of all your friends, linking two people with a blue edge if they are friends and with a red edge if they are strangers. Then you might end up with something like this:
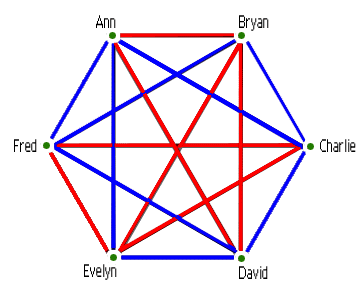
Now this looks pretty complicated and it would take quite a lot of information to describe who is connected by red edges and who is connected by blue edges. But if you zoom in on just Ann, Bryan and David, they are all joined by red edges. This red triangle is an example of order hiding in the messy overall network. The more ordered a system is, the simpler its description. The most ordered friendship network is one that has all the edges the same colour: that is, everyone is friends or everyone is strangers.
Ramsey discovered that no matter how much order you were looking for – whether it was three people who were all friends and strangers or twenty people who were all friends and strangers – you were guaranteed to find it as long as the system you were looking in was large enough. To guarantee yourself a group of three people who are all friends or all strangers you need a friendship network of six people: five people isn't enough as this counterexample shows.
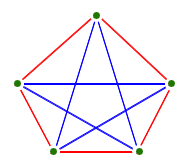
The number of people you need to guarantee that you'll find three friends or three strangers is called the Ramsey number R(3,3). We know a few Ramsey numbers: we've seen that R(3,3)=6, and it has been proved that R(4,4), the number of people you need to guarantee you'll find four friends or four strangers, is 18. But we hit a wall very quickly. For example we don't know what R(5,5) is. We know it's somewhere between 43 and 49 but that's as close as we can get for now.
Part of the problem is that numbers in Ramsey theory grow incredibly large very quickly. If we are looking at the relationships between three people, our network has just three edges and there are a reasonable 23 possible ways of colouring the network. For four people there are six edges and 26=64 possible colourings. But for the relationships between six people there are fifteen edges and we already have to consider an unwieldy 215=32,768 possible colourings. Mathematicians are fairly certain that R(5,5) is equal to 43 but haven't found a way to prove it. One option would be to check all the possible colourings for a network of 43 people. But each of these has 903 edges, so you'd have to check through all of the 2903 possible colourings – more colourings than there are atoms in the observable Universe!
Too big to write but not too big for Graham
Big numbers have always been a part of Ramsey theory but in 1971 mathematician Ronald Graham came up with a number that dwarfed all before it. He established an upper bound for a problem in the area that was, at the time, the biggest explicitly defined number ever published. Rather than drawing networks of the relationships between people on a flat piece of paper as we have done so far, Graham was interested in networks in which the people were sitting on the corners of a cube.
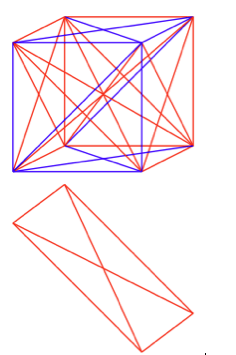
In this picture we can see that for a particular flat diagonal slice through the cube, one that contains four of the corners, all of the edges are red. But not all colourings of a three-dimensional cubes have such a single-coloured slice. Luckily, though, mathematicians also have a way of thinking of higher dimensional cubes. The higher the dimension, the more corners there are: a three-dimensional cube has 8 corners, a four-dimensional cube has 16 corners, a five-dimensional cube has 32 corners and so on. Graham wanted to know how big the dimension of the cube had to be to guarantee that a single-coloured slice exists.

Ronald Graham who gave us his beautiful number. Image: Cheryl Graham.
Graham managed to find a number that guaranteed such a slice existed for a cube of that dimension. But this number, as we mentioned earlier, was absolutely massive, so big it is too big to write within the observable Universe. Graham was, however, able to explicitly define this number using an ingenious notation called up-arrow notation that extends our common arithmetic operations of addition, multiplication and exponentiation.
We can think of multiplication as repeated addition:
3 x 3 = 3+3+3
33 = 3 x 3 x 3.
If we define the single arrow operation, ↑, to be exponentiation, so:
3↑3 = 33 = 3 x 3 x 3 = 27,
then we can define the double-arrow operation ↑↑ to be
3↑↑3 = 3↑3↑3 = 333 = 327 = 7,625,597,484,987.
We can carry on building new operations by repeating previous ones. The next would be the triple-arrow
3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑↑3)=3↑↑7,625,597,484,987
a tower of powers of 3 that is 7,625,597,484,987 levels high! (See here to read about the up-arrow notation in more detail.)
The number that has come to be known as Graham's number (not the exact number that appeared in his initial paper, it is a slightly larger and slightly easier to define number that he explained to Martin Gardner shortly afterwards) is defined by using this up-arrow notation, in a cumulative process that creates power towers of threes that quickly spiral beyond any magnitudes we can imagine.
But the thing that we love about Graham's number is that this unimaginably large quantity isn't some theoretical concept: it's an exact number. We know it's a whole number, in fact it's easy to see this number is a multiple of three because of the way it is defined as a tower of powers of three. And mathematicians have learnt a lot about the processes used to define Graham's number, including the fact that once a power tower is tall enough the right-most decimal digits will eventually remain the same, no matter how matter how many more levels you add to your tower of powers. Graham's number may be too big to write, but we know it ends in seven. Mathematics has the power not only to define the unimaginable but to investigate it too.
About this article

Rachel Thomas and Marianne Freiberger are the editors of Plus. This article is an edited extract from their new book Numericon: A journey through the hidden lives of numbers.
Comments
Nic
Why did he stop in g64 and not in g43,670 or g589,007?
Oliver
Which number is bigger, Grahams number of googolplexianth (10^googolpleian)