Classroom activity: the game of life

One of the amazing things about life is its sheer complexity. How can a bunch of mindless cells combine to form something as complex as the human brain, or as delicate, beautiful and highly organised as the patterns on a butterfly's wing? Is there any hope of ever describing the processes involved and improving our understanding of living organisms?

Well, so far no-one has cracked the secret of life completely, but mathematics gives some interesting insights. One of them is that complexity can arise from some very simple rules. In this activity we'll look at a famous illustration of this fact, the game of life, which was invented by the mathematician John Conway in 1970. It's not a game in the usual sense because there's only one player. All you do is set the scene and watch the game evolve.

The game is played on a chequerboard (click on the button on the right to open the grid). Initially, some of the squares contain an "organism" and some don't (by clicking on the squares you can choose which ones contain the blue organisms). Each square has eight neighbours, one on top, one below, one left, one right and four at the corners. At the next step, new organisms are born, die or survive according to the following simple rules:

• Every organism whose eight neighbouring squares contain only one other organism, or none at all, dies from loneliness. It disappears at the next step.
• Every organism with four or more neighbouring organisms dies from over-population, it'll also disappear.
• Every organism with two or three neighboring organisms survives.
• Each empty square that's adjacent to exactly three squares containing organisms is a birth square. A new organism will appear in it at the next move.

You can explore the Game of Life in the interactivity below, created by our amazing colleague Oscar Gillespie. It starts off with a random pattern of live cells. If you would instead like to choose your own starting arrangement of live cells, click Clear the grid and then click on the individual cells you would like to be live. To run just a single step of the Game of Life, click on Run a generation. To run through many steps, click Run. And to start again, click Stop and then Reset.

To find out more about the Game of Life and the motivation behind it in Conway's own words, see our article Games, life and the game of life. 

Here are some questions to ponder:

• Can you find initial patterns which always die out completely, no matter how many organisms there were to start with?
• Can you find an initial pattern that remains exactly the same over all generations?
• Can you find an initial pattern that gives an oscillation between two patterns, that is, a pattern that changes to another pattern at the first step and then comes back to itself?
• Generally, what tends to happen to most initial patterns?

(See here for some answers.)

And here are some interesting initial patterns to play with:

• The pulsar

  

  The pulsar

  
   

• A tetromino

  

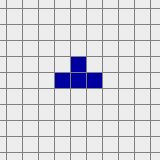
  A tetromino

  
   

• A diehard

  

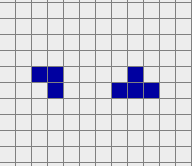
  A diehard

  
   

• A glider

  

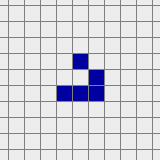
  A glider

• A gun

  

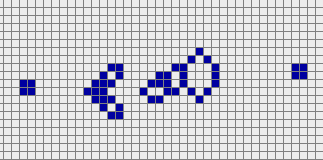
  A gun

Conway's game of life shows that even very simple rules can produce a large variety of different behaviours, including highly organised and very complex ones. What's amazing is this wasn't what Conway set out to show when he designed the game — what he was really after was an infinitely programmable computer. Find out more in our interview with Conway.