Plus Advent Calendar Door #19: Beautiful buildings

The dramatic curved surfaces of some of the iconic buildings created in the last decade, such as 30 St Mary's Axe (AKA the Gherkin) in London, are only logistically and economically possible thanks to mathematics. Curved panels of glass or other material are expensive to manufacture and to fit. Surprisingly, the curved surface of the Gherkin has been created almost entirely out of flat panels of glass — the only curved piece is the cap on the very top of the building. And simple geometry is all that is required to understand how.

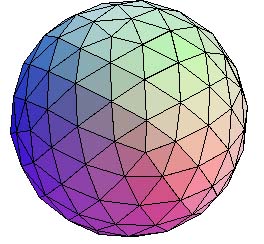
A geodesic sphere.

One way of approximating a curved surface using flat panels is using the concept of geodesic domes and surfaces. A geodesic is just a line between two points that follows the shortest possible distance — on the Earth the geodesic lines are great circles, such as the lines of longitude or the routes aircraft use for long distances. A geodesic dome is created from a lattice of geodesics that intersect to cover the curved surface with triangles. The mathematician Buckminster Fuller perfected the mathematical ideas behind geodesic domes and hoped that their properties — greater strength and space for minimum weight — might be the future of housing.

To try to build a sphere out of flat panels, such as a geodesic sphere, you first need to imagine an icosahedron (a polyhedron made up of 20 faces that are equilateral triangles) sitting just inside your sphere, so that the points of the icosahedron just touch the sphere's surface. An icosahedron, with its relatively large flat sides, isn't going to fool anyone into thinking it's curved. You need to use smaller flat panels and a lot more of them.

Divide each edge of the icosahedron in half, and join the points, dividing each of the icosahedron's faces into four smaller triangles. Projecting the vertices of these triangles onto the sphere (pushing them out a little til they two just touch the sphere's surface) now gives you a polyhedron with 80 triangular faces (which are no longer equilateral triangles) that gives a much more convincing approximation of the curved surface of the sphere. You can carry on in this way, dividing the edges in half and creating more triangular faces, until the surface made up of flat triangles is as close to a curved surface as you would like.

Find out more about the Gherkin and other iconic buildings on Plus.

Return to the Plus Advent Calendar