Mathematicians rival octopus in World Cup final prediction

A new mathematical analysis of team tactics predicts a Spanish win in Sunday's FIFA World Cup final and also sheds some light on why England were trashed by Germany.

Mathematicians and football supporters Dr Javier López Peña and Dr Hugo Touchette from Queen Mary, University of London have collected ball passing data from all of the FIFA World Cup games and analysed it to reveal the nations' different styles of play.

Using the mathematical technique called graph theory, they have revealed the gaping holes in England's tactics against Germany and made predictions about the Netherlands-Spain final that may just rival the psychic octopus.

For each national side, López Peña and Touchette have drawn up a network of passes between players throughout the tournament and analysed how these networks compare between teams. Touchette explains: "Each player in the network is given a score called centrality, which measures how vital they are to the network. The higher the centrality score, the bigger the impact if that player wasn't there. This method is most commonly used to make computer networks more robust, but it can also be used to plan football strategy."

The Netherlands-Spain prediction

The networks reveal that Spanish players have made a strikingly high number of passes in this tournament, almost 40% more than Germany and twice as many as the Dutch. "The team relies on swift passes that are well distributed among all players, especially between those playing mid-field," said López Peña.

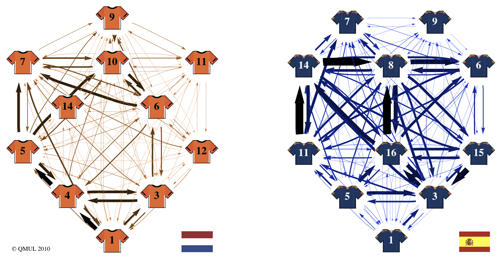
David Villa (number 7), the tournament's highest goal scorer, has received an average of 37 passes per game, more than any other forward from all the teams. López Peña said: "Villa's performance has been impressive compared with Fernando Torres (number 9), who has not scored any goals this tournament. This was reflected in the successful Spanish tactics, with Torres only receiving an average of 13 passes per match, and 37 to Villa."

Conversely, the Dutch game play is clearly offensive, involving a very low number of passes between players, most of which are aimed at the strikers. López Peña said: "The low number of passes shows the Dutch prefer quick attacks and counterstrikes rather than intricate playing. Their goals are often scored from set pieces such as free kicks and they use their physical presence to beat their opponents."

The England-Germany match

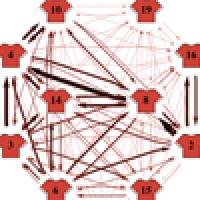
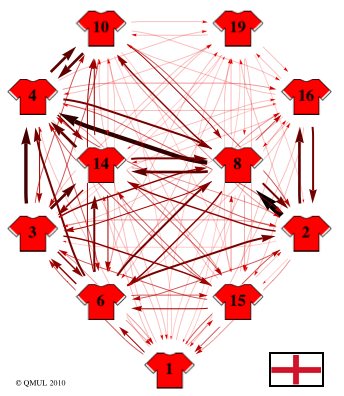
The analysis shows the English squad to have a balanced line-up with no single player more important than the team as a whole. López Peña said: "The good midfield work of Frank Lampard (number 8), Steven Gerrard (number 4) and Gareth Barry (number 14) doesn't appear to transfer very well to the forwards, with Wayne Rooney (number 10) receiving on average three times more passes than Jermain Defoe (number 19). This makes the English attack very predictable and easily stoppable by blocking Rooney, who is usually forced to give the ball back to Gerrard."

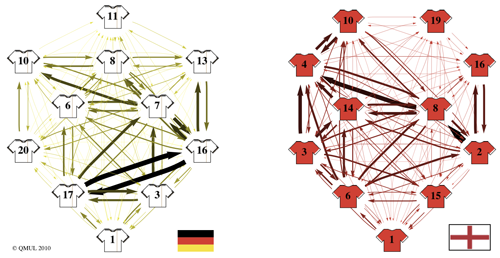
The German network appears even more balanced than the English one, with a higher number of passes, suggesting more circulation of the ball. "Particularly relevant are the passes between Philipp Lahm (number 16) and Bastian Schweinsteiger (number 7) and most of the German attacks are built up from the defenders. Mesut Oezil (number 8) makes good work connecting both sides of the field on the attack, making the German offensive game very effective and hard to defend against. The key player in the German strategy remains Schweinsteiger, who was effectively blocked by the Spanish midfielders' characteristic fast circulation in their semi-final defeat," said López Peña.

For more graphs and more information see the researchers' website.

Adapted from press release by Matt Parker and Simon Levey