
The maths of February 29
The year 2020 is longer than 2019: since 2020 is a leap year, February has one day more than usual. Why does the calendar work this way?
Well, basically it is all to do with the rotation of the Earth around the Sun (or, for pre-Copernicans, the rotation of the Sun around the Earth). We have 365 days in an ordinary year, but the period of the Earth's orbit is close to 365¼ days. This means that, if there were no leap years, every four years the seasons would be displaced by roughly one day, and so spring would come later and later in the calendar as the years passed.
The length of a year is roughly the time it takes for the Earth (third planet from the centre) to move around the Sun once. (Image courtesy: NASA/JPL.)
To deal with this problem, the Roman leader Julius Caesar (advised by the mathematician Sosigenes) reformed the calendar in 46BC, so that, after every three years with 365 days, there was a fourth year with 366. At the time, calendars with 365-day years were in use in Persia and Egypt, and these calendars showed the seasonal slipping effects due to the discrepancy between the calendar and solar years. The Romans had previously had a more complicated system which might have avoided the slippage: they alternated years of 355 days with years containing an extra, intercalary, month of either 22 or 23 days This system potentially could have kept the calendar in step with the seasons, but the interpolations were not always regular, because they were determined by priests who sometimes had political reasons for shortening or lengthening the year.
Caesar's innovation resulted in a calendar — the Julian calendar — in which every fourth year was a leap year with an extra day. This was reasonably consistent with the apparent motion of the sun in the short term. But the solar year — the time between successive spring equinoxes — is actually slightly shorter than 365¼ days, so over the centuries the seasons measured by the calendar would start slightly earlier than in reality. By the sixteenth century, the discrepancy, which by now amounted to ten days, was clear. This had practical implications: some parts of the church used the spring equinox (determined by the Sun) to calculate the date of Easter, while the Church of Rome used March 25 (given by the calendar) in its calculation, with the result that the calendar drift meant that not all Christians were celebrating Easter on the same day. To address this problem, Pope Gregory XIII in 1582 introduced a calendar reform: instead of every fourth year being a leap year, century years would not be leap years unless the year number was divisible by 400. This reduced the mean calendar year from 365.25 days to 365.2425 days, a 0.002% correction which brought the calendar year closer to the solar year.
The Gregorian calendar
The new Gregorian calendar was adopted in the states under the Pope's rule by the mechanism that Thursday 4 October 1582 was followed by Friday 15 October, thus deleting ten days from 1582. (As it happens, the Spanish mystic Saint Teresa of Avila died on the night in question, either just before midnight on 4 October or on the morning of 15 October.)
For a time Protestant countries stuck with the Julian calendar. Queen Elizabeth of England asked the mathematician John Dee to advise on calendar reform — he proposed a different solution, losing eleven days rather than Gregory's ten — but it was not until 1752 that the United Kingdom switched to the Gregorian calendar, with Wednesday 2 September being followed by Thursday 14 September. Cutting out eleven days brought the British calendar in line with the continental Gregorian calendar: while the Papal States had lost only ten days, the discrepancy by 1752 had increased to eleven since 1700 was a leap year in the Julian calendar but not in the Gregorian.
Between 1582 and 1752 the British calendar was behind that in use in Catholic countries. So although the two great writers Miguel de Cervantes and William Shakespeare both died on 23 April 1616, Cervantes, in Catholic Spain with the Gregorian calendar, died ten days before Shakespeare whose death was recorded under the Julian calendar.
What day is your birthday?
One consequence of the adoption of the Gregorian calendar relates to the frequencies of the days of the week on which a given date occurs.
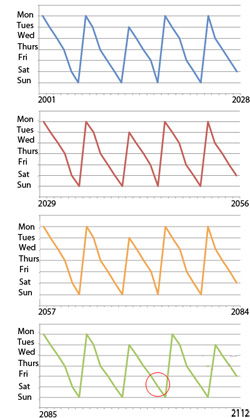
Suppose your birthday is January 1st. In 2001 that would have been a Monday. The charts show the days of the week your birthday would have been in the subsequent years (in the Gregorian calendar). You can see that the pattern repeats every 28 years, from 2001 to 2084. The next 28-year period contains a century year (2100), which should be a leap year, but isn't. Therefore it breaks the cycle (see red circle). You have to wait 400 years for the pattern to repeat exactly. Click here for a larger image.
The number 365 is one more than a multiple of 7 (365 = 7 x 52 + 1) which means that, in a non-leap year your birthday advances by one day of the week: that is, if in 2014 your birthday was on a Monday, in 2015 it was on a Tuesday. If there were no leap years, your birthday would progress one day at a time for as long as you lived. But leap years change that: they mean that your birthday jumps forward two days. (Whether that happens in the leap year itself, or in the following year, depends on whether you were born between March and December or in January or February.)
The Julian calendar essentially operates a repeating cycle of four years, three of 365 days followed by one of 366. The total length of these four years is 1461 days. This is equal to 7 x 208 + 5 days, and because this length isn't divisible by 7, it takes seven four-year cycles before the sequence of days for a given date, such as your birthday, repeats. Over these 28 years, your birthday will occur four times on each of the days of the week.
Think now of the Gregorian calendar. Because of the different treatment of century years, it repeats every 400 years. These 400 years contain 303 non-leap years of 365 days and 97 leap years of 366 (since only one of the four century years is a leap year). That is a total of 146,097 days, and it happens that 146,097 is an exact multiple of 7 – it is 7 times 20,871.
This is significant because it means that, every 400 years, the pattern of days restarts from the same point. If you were born on Monday 1 January 2001, say, then your birthday would fall on the same day of the week in 2401, 2801, 3201 and so on. By 1 January 2084 you would have had 12 Monday birthdays, 12 Tuesday and so on. But the century years break that uniform pattern, and over the four hundred years 2001-2400 your birthdays will fall on 56 Mondays, 58 Tuesdays, 57 Wednesdays, 57 Thursdays, 58 Fridays, 56 Saturdays and 58 Sundays. Since 1 January 2401 is again a Monday, this cycle will repeat in perpetuity.
Friday the 13th
For the superstitious, there is an unfortunate curiosity resulting from this property that the period of the Gregorian calendar is exactly divisible by 7. It is traditionally unlucky when the 13th of a month falls on a Friday. Under the Julian calendar, the 13ths of each month fall uniformly amongst all the weekdays so that on average, exactly one month out of every seven would include a Friday the 13th. But the Gregorian calendar loses this uniformity, and in fact it turns out that the most common weekday for the 13th of a month to fall on is a Friday! (Of course, it's arguable that we shouldn’t make too much of this statistical preponderance when we haven't yet completed one full 400-year cycle of the calendar on which it relies!)
What if you were born on February 29?
Now some people happen to be born on 29 February (which, if births were uniform throughout the year, would be 1 person in every 1461). If by "birthday" one means "the calendar date on which one was born", then these unfortunate people have less frequent birthdays than the rest of us. In practice, they may choose to celebrate the anniversary of their birth on 28 February or 1 March (depending on the country, they legally come of age on one or other of these dates) and so hopefully they don't miss out on the cake, candles and presents. But they can celebrate on the exact date of their birth at most one year in four.

If you were born on February 29 you age more slowly!
For example, the composer Gioachino Rossini (who wrote the opera The Barber of Seville and many others) was born on 29 February 1792. He had a birthday in 1796, but 1800 wasn't a leap year and his second exact birthday wasn't until 1804. He wrote his last opera, William Tell, in 1829 — before his ninth birthday! So when was Rossini's fiftieth exact birthday? Since 1800 and 1900 were not leap years, this anniversary didn't happen until 2000 – which of course was a leap year, since 400 divides 2000. (Incidentally, Rossini died on a Friday 13, so that calendar superstition proved unlucky for him.)
Those born on 29th February have fewer occurrence of their birth dates. If they were living in Sweden in the years after 1700, there were additional factors involved. Sweden decided to move towards the Gregorian calendar in 1700, but chose to do so by losing 11 days, not in a single step as generally happened elsewhere, but by having no leap years between 1700 and 1740 inclusive, So if you had happened to be born in Sweden on 29 February 1696, under this system you would have had to wait until 1744 for your first birthday! But in 1712, the change having been badly implemented (1704 and 1708 had both been leap years when they should not have been), it was abandoned and Sweden returned to the Julian calendar. This was done by introducing an extra day into February 1712 to bring the calendars back into line, to make up for the non-Julian leap year that had occurred in 1700. So those people born on 30 February 1712 in Sweden never had the opportunity to celebrate a real birthday!
Further reading
David Ewing Duncan, The Calendar, Fourth Estate, 1998
About this article
This article has described some of the mathematics behind calendar reform, and the consequences of the arithmetic of extra, intercalary, days. For a more extended account of this topic, watch Tony Mann's Gresham College lecture. It's a free public lecture that will be held in London at 6pm on February 29th 2016. After that a video of the lecture will be available on the Gresham College website.

Tony Mann is Director of Greenwich Maths Centre and has taught mathematics at the University of Greenwich for many years. He was Visiting Professor of Computing Mathematics at Gresham College from 2012 to 2015 and is a former President of the British Society for the History of Mathematics.
Comments
Anonymous
The Orthodox church kept to the Julian calendar until after the 1917 revolution (the calendar changed in 1918, with the first day of February 1918 being the 14th). So the October Revolution actually happened in November (by the Gregorian calendar).
Anonymous
Having been born on 2/29/48, this article is certainly relevant to me. I'm always the youngest person of the people born the same year as I. We also can look forward to the day when, due to the Earth's slowing rotation, when the solar year will be exactly 365.25 days long and we can have centenary years not divisible by 400 have a leap year. I was lucky in 2000.
Anonymous
So inaccurate, it they had to resort to leap year shenanigans to re-calibrate it once in a while.
The Mayans had a 260 days calendar, which was far better synchronized with the solar cycle and the human body.
And for practical purposes, the lunar calendar was better, especially for the farmers who need to know precisely when to plant and harvest.
Anonymous
i'm a farmer and i'm more partial to the Mayan Calendar