Happy pi day 2016!
It's March 14th, which in the US is written as 3/14 — and since 3.14 are the first three digits of that most famous of mathematical constants, $\pi$, today is celebrated internationally as pi day.
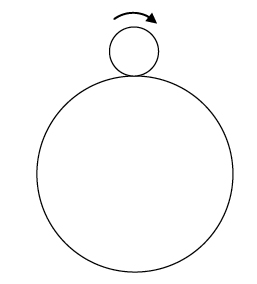The number $\pi$ is the ratio of the circumference of a circle to its diameter. To celebrate this lovely number, here's a little puzzle to ponder. Imagine a circle with radius 1 cm rolling completely along the circumference of a circle with radius 4 cm. How many rotations does the smaller circle make?
The circumference of a circle with radius $r$ is $2\pi r$, so the circumference of a circle with radius $4r$ would be $8\pi r$. Since
$8\pi r \div 2\pi r = 4,$
it seems the answer must be four revolutions. But that's not true! The answer is actually 5! Can you figure out why?
How many revolutions will the smaller circle make when rolling around the bigger one?
We found out about this curious question from Yutaka Nishiyama, a mathematical friend in Japan. You can read about the answer in his article Circles rolling on circles. Happy puzzling!
math.nights
To Arabic: https://goo.gl/l3Mt0L
Anonymous
Thank you for translation in Arabic.
Yutaka Nishiyama
Anonymous
The additional rotation occurs because the smaller circle traverses the circumference of the larger circle, in the same way that the moon rotates once every time it orbits the Earth, even though it maintains the same face towards the Earth. Of course, this assumes that the smaller circle moves as well as rotates, and that the larger circle neither moves nor rotates. If the centres of the two circles are fixed and both are free to rotate, as gears, then the answer will be 4, not 5. Furthermore, if your frame of reference is the larger circle and that circle is allowed to both move and rotate, then it is possible to envisage the smaller circle appearing to rotate 4 times without it moving or rotating at all! - Paul Baron
Anonymous
The question without the accompanying diagram could also mean to roll the small circle within the larger one. If this is done you actually lose a rotation. The answer then is 3!
The easiest way to calculate the rotations is to use the path taken by the centre of the small circle.
If r[1] = radius of small circle; r[2] = radius of path outside and r[3] = radius of path inside the large circle then:-
Rotations outside = (2 x pi x r[2])/(2 x pi x r[1]) = (2 x pi x 5)/(2 x pi x 1) = 5/1 = 5.
Rotations inside = (2 x pi x r[3])/(2 x pi x r[1]) = (2 x pi x 3)/(2 x pi x 1) = 3/1 = 3.
K. Selby