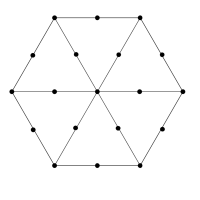
Magic 19
Here are 19 dots arranged in a hexagon. Your task is to label the dots with the numbers 1 to 19 so that each set of three dots that lie along a straight-line segment add up to 22.
Happy puzzling!
(Download the grid to print and scribble on.)
Solution link
Michail Polykretis
Evert van Dijken
This is an excellent problem to solve as an LP-problem.
Semidán
A bit late, but here it is. Concretely, an Integer Linear Program. Also includes another program to find alternative solutions. Both implemented in R!
Best
Semidán
https://github.com/Robaina/Magic-N-gon
Alex Zeffertt
I avoided using a computer - it's more fun as a logic puzzle. The trick is to start with 3-18-1-19-2, which has to be there somewhere. Then, name the points x (centre), y_i (degree 2 node on spokes), z_i (degree 3 node on spokes), w_i (degree 2 node on rim). Then create equations for the sum of the outer segments, the sum of all segments, and the sum of all nodes. These show x must be even, which means it can't be 1 or 3. So either 2 is at the centre, or 4 (since either 2-17-3 or 1-17-4 must appear). Then you need to take advantage of the fact that there are 10 odd numbers and the number of odd numbers in y_i and z_i must match. You also need to use the fact around any triangle there must be either 0 or 2 odd numbers in the middle of the edges. This ultimately leads to ruling out 2 at the centre, and eventually you find the result with 4 at the centre.
What I really want to know... is how did the question setter know there would be a solution?