
Coding theory: the first 50 years
In recent weeks people all over the world have been fascinated by the pictures and scientific data being relayed from Mars by NASA's Pathfinder mission. For decades space probes have been sending back similar data from the furthest planets. Yet the power of the radio transmitters on these craft is only a few watts, comparable to the strength of a dim electric light bulb. How can this information be reliably transmitted across hundreds of millions of miles without being completely swamped by noise?


The Sojourner rover and Mars Pathfinder lander (as seen from the rover). The circular high-gain antenna is pointing towards Earth.
(Source: Jet Propulsion Laboratory, NASA.)
Many different disciplines come together to successfully recover these signals — electronic engineering, computing and mathematics.
Coding theory is the branch of mathematics concerned with transmitting data across noisy channels and recovering the message. Coding theory is about making messages easy to read: don't confuse it with cryptography which is the art of making messages hard to read!
We assume that our message is in the form of binary digits or bits, strings of 0 or 1. We have to transmit these bits along a channel (such as a telephone line) in which errors occur randomly, but at a predictable overall rate. To compensate for the errors we need to transmit more bits than there are in the original message.
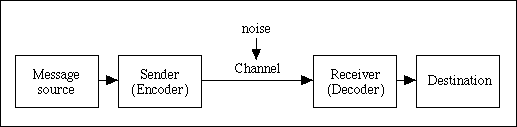
A channel.
The simplest method for detecting errors in binary data is the parity code which transmits an extra "parity" bit after every 7 bits from the source message. However, this method can only detect errors, the only way to correct them is to ask for the data to be transmitted again!
A simple way to correct as well as detect errors is to repeat each bit a set number of times. The recipient sees which value, 0 or 1, occurs more often and assumes that that was the intended bit. The scheme can tolerate error rates up to 1 error in every 2 bits transmitted at the expense of increasing the amount of repetition.
Early days
The disadvantage of the repetition scheme is that it multiplies the number of bits transmitted by a factor which may prove unacceptably high. In 1948, Claude Shannon, working at Bell Laboratories in the USA, inaugurated the whole subject of coding theory by showing that it was possible to encode messages in such a way that the number of extra bits transmitted was as small as possible. Unfortunately his proof did not give any explicit recipes for these optimal codes.
It was two years later that Richard Hamming, also at Bell Labs, began studying explicit error-correcting codes with information transmission rates more efficient than simple repetition.[Correction]. His first attempt produced a code in which four data bits were followed by three check bits which allowed not only the detection but the correction of a single error. (The repetition code would require nine check bits to achieve this.)
It is said that Hamming invented his code after several attempts to punch out a message on paper tape using the parity code. "If it can detect the error," he complained, "why can't it correct it!".
While Shannon and Hamming were working on information transmission in the States, John Leech invented similar codes while working on Group Theory at Cambridge. This research included work on the sphere packing problem (see this issue's mathematical mystery) and culminated in the remarkable, 24-dimensional Leech lattice, the study of which was a key element in the programme to understand and classify finite symmetry groups.
Applications

The North polar cap of Mars, taken by Mariner 9 in 1972. (Source: NASA.)
The value of error-correcting codes for information transmission, both on Earth and from space, was immediately apparent, and a wide variety of codes were constructed which achieved both economy of transmission and error-correction capacity. Between 1969 and 1973 the NASA Mariner probes used a powerful Reed-Muller code capable of correcting 7 errors out of 32 bits transmitted,
consisting now of 6 data bits and 26 check bits! Over 16,000 bits per second were relayed back to Earth.

A less obvious application of error-correcting codes came with the development of the compact disc. On CDs the signal in encoded digitally. To guard against scratches, cracks and similar damage two "interleaved" codes which can correct up to 4,000 consecutive errors (about 2.5 mm of track) are used. (Audio disc players can recover from even more damage by interpolating the signal.)
Modern developments
In the past two years the goal of finding explicit codes which reach the limits predicted by Shannon's original work has been achieved. The constructions require techniques from a surprisingly wide range of pure mathematics: linear algebra, the theory of fields and algebraic geometry all play a vital role. Not only has coding theory helped to solve problems of vital importance in the world outside mathematics, it has enriched other branches of mathematics, with new problems as well as new solutions.
Further reading
The mathematics of error-correcting codes is discussed by
- Charles Goldie and Richard Pinch, Communication theory, Cambridge University Press, 1992
- Dominic Welsh, Codes and cryptography, Oxford University Press, 1988
- Ray Hill, A first course in coding theory, Oxford University Press, 1986
More information about the Mars Pathfinder Mission is available from the "Mars Missions" web site.
Biographies of the mathematicians mentioned in the article are available from the "MacTutor history of mathematics archive":
The author
Dr Richard Pinch, Department of Pure Mathematics and Mathematical Statistics, University of Cambridge
Correction
Since publication of this article, following comments from a reader, the author has requested the following amendment:
Two years later, Hamming, also at Bell Labs, published details of his work on explicit error-correcting codes with information transmission rates more efficient than simple repetition.
The Letters page of PASS Maths Issue No 5: May 1998 contains the reader's comments and author's response.
Comments
V'Ger
Is this related to Golay-codes? If so, how?