This article first appeared on the FQXi community website. FQXi are our partners in our Who's watching? The physics of observers project, within which we explore quantum contextuality. Click here to find out more about contextuality.

Is the concept of an omniscient God compatible with the laws of physics? In the 1960s, Swiss mathematician Ernst Specker set out to find the answer. His investigation led him, along with American mathematician Simon Kochen, to codify one of the strangest rules of quantum reality: contextuality.

To understand the oddness of contextually, imagine that choosing to step on the scale and measure your weight could change your eye color. That's the everyday equivalent of what seems to happen when we decide how to measure the quantum properties of a particle.

Jan-Åke Larsson, Adán Cabello, Mile Gu, Karoline Wiesner, & Otfried Gühne at a quantum contextuality workshop in Siegen, September 2014. Image: Alex Monrás

Physicists Otfried Gühne, at the University of Siegen, in Germany, Adán Cabello, at the University of Seville, in Spain, and Jan-Åke Larsson, at the University of Linköping, in Sweden, are investigating this surprising brand of quantum weirdness. The team is looking to the future to see if quantum contextuality could one day drive more powerful computation. They are also digging back into the past to learn about the religious quest that led to the concept of contextually.

Quantum coin flipping

Quantum theory often feels like a piling-on of the bizarre. We're told, for instance, that the simple act of making a measurement can change a particle's state in an unpredictable manner. But contextuality is a fresh violation of our intuition about how the world is supposed to work. To illustrate just how counterintuitive it is, Larsson offers the example of a coin flip. Imagine taking three coins from your pocket—a penny, a nickel, and a dime, for example—and flipping any two of them. Say that you choose to flip the penny and the dime. The outcome of the dime flip shouldn't depend on whether you flipped it along with the penny or along with the nickel—and, of course, in the everyday world, it does not.

Now transpose this scenario to the quantum world. Instead of pulling two of three coins from your pocket, imagine that you have a particle on which you can make two of three possible measurements. The measurements are all of the same property, a quantity called the magnetic quadrupole moment (which is equivalent to the value of the particle's spin, squared). The quadrupole moment is three-dimensional, and you can choose two of three axes along which to measure it: the x-axis, the y-axis, and a third which is 45 degrees away from the y-axis but still perpendicular to the x-axis. Just like the coin toss, you don't expect that your choice to measure along the second or third axes should affect the result you get for the measurement along x-axis. Yet, in the quantum world, it does. This strange link between the choice of one measurement and the result of a second is called contextually.

Though physicists had suspected that quantum contextually might hold since the early days of the field, the idea wasn't formally described until 1967, when Kochen and Specker devised a mathematically elegant proof. The duo wanted to see if a more intuitive deterministic picture of reality—such as the one preferred by Einstein—could explain the outcome of particle experiments. In this view, particles do not pick their properties in an instant, at the point of measurement, apparently on a whim, as standard quantum theory asserts. Instead, the particles contain "hidden variables" that determine the outcome of any future measurements in a predictable manner. These hidden variables provide a complicated set of instructions, even pre-programming particles to return different responses to the same measurement, depending on the order in which measurements are carried out—thus mimicking contextuality. But crucially, since experimenters have no access to these hidden variables, to them, the results appear to be mysterious and are impossible to predict before the experiment is performed.

With their theorem, Kochen and Specker showed that such "non-contextual" theories that invoke hidden variables cannot explain the outcome of quantum measurements without hitting a paradox. The mathematicians achieved this by considering how such information might be stored within a single particle, and proved that there's simply no way to encode these instructions so that you cover every possible different result that could be seen in an experiment. These theories are fundamentally at odds with quantum mechanics.

But to test the Kochen-Specker theorem, physicists would have to make a series of simultaneous (or nearly simultaneous) measurements on a single particle. This experiment was out of reach when the theorem was first published because, at the time, measuring the state of a particle demolished it, preventing further tests. "It's a very beautiful result, but it's a mathematical one," says Cabello. With no way to test the theorem experimentally, it languished for almost 40 years.

Non-demolition measurements

Finally, around 2003, a new delicate technique for making "non-demolition measurements" enabled physicists to test the theorem for the first time. It allowed physicists to preserve the state of an ion in a trap, even after measuring it. In 2009, Cabello and his colleagues performed the first lab experiment affirming a simplified form of the Kochen-Specker theorem. A more rigorous test, also by Cabello and colleagues, following exactly the measurements that Kochen and Specker laid out, came in 2013.

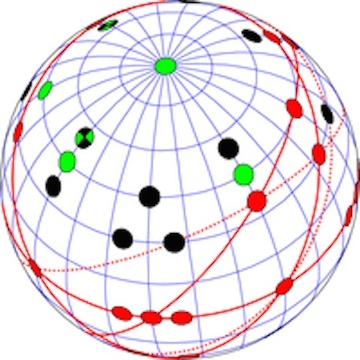
The Kochen Specker theorem considers a number of directions along which a particle's properties can be fixed before measurement. Image: Jan-Åke Larsson

"Vindication" was Cabello's first reaction, he recalls. But this was only the beginning. "Now I realise they provided the ground needed for the next set of questions: why quantum theory is as contextual as it is? What is quantum theory really telling us about the world?"

To answer those questions, Gühne, Cabello, and Larsson must address the gap between ideal experiments, in which measurements are made simultaneously, and real ones, in which the measurements are made in sequence. "When you do these measurements, you can't perform them ideally. That's a fact of life," says Larsson. "There can be delays—will be delays—between the detector that measures one property and the one that measures the other." What inaccuracies might follow from these delays? That is something that the researchers are now trying to figure out.

Bizarre as it seems, contextuality may also provide insight into why quantum computers could be so powerful at solving certain classes of problems. Despite decades of progress in building quantum computers, physicists still disagree about exactly which quantum effect gives them an edge. Last year, a team of researchers from Ireland and Canada argued in Nature that contextually is the critical ingredient driving error correction in quantum computers. But some argue that contextually may even be the source of the speed-up that would make quantum computers outperform classical machines. (See also, Quantum in context.) The connection between the power of quantum computers and contextuality "is almost one-to-one," says Cabello. "You have this power because you have this magic."

The practical benefits of contextuality are still up for discussion among researchers who have been meeting regularly at a series of FQXi-funded workshops in Spain, Germany, Singapore, and Sweden. "Definitely we had a heated debate on contextually," says FQXi member Pawel Kurzynski, a physicist at the Centre for Quantum Technologies (CQT) at the National University of Singapore, who participated in the Spanish workshop, and co-organised the Singapore meeting.

The Swedish meeting, which took place in August 2015, emphasised the philosophy and history of field. Cabello has recorded about a dozen video interviews with key contextuality researchers so far, including Kochen and Specker (Specker died in 2011). "You start filming, and there's always some point at which you capture something special," says Cabello.

God's omniscience?

It was through these interviews that Cabello discovered that Specker wanted to study quantum reality—whether it was indeterministic, as standard quantum theory asserts, or could instead be described by a deterministic hidden-variables theory—in part, to better understand deep religious questions. Could God be omniscient, if reality itself is not set until it is observed by humans?

Cabello believes that contextuality does not force physicists to give up a belief that there is real world out there. But perhaps it is not as concrete as some might wish. "We do believe in a reality," says Cabello. "An electron has an electric charge, for instance." But other properties of the quantum system have no deeper reality; they are created by the act of measurement, he says.

Gühne, Cabello, Larsson and their colleagues underscore that view with new research uncovering flaws in those interpretations of quantum mechanics that assume that the quantum properties we measure are reflections of some intrinsic reality that exists independently of the act of measuring. Their conclusion comes from an unlikely source: thermodynamics, the same branch of physics that describes classical systems like steam engines. They found that, under certain assumptions, if quantum probabilities are determined by intrinsic properties, a quantum system could release infinite heat with each successive measurement. This rules out such models. "Ultimately," they write, "our work indicates that the long-standing question, 'Do the outcomes of experiments on quantum systems correspond to intrinsic properties?' is not purely metaphysical."

The team now aims to create a web archive of their contextulaity video interviews, for both experts and the general public. "Many scientists are not really interested in history of science because they are absorbed in their daily research," says FQXi member Dagomir Kaszlikowski, a contextually expert also at CQT. But, he adds—possibly with an intentional pun—knowing the historical "context" of the theory's origins is crucial, to avoid misunderstanding what it is really about.