Colouring by numbers: The Kochen-Specker theorem

We have seen in a previous article that quantum mechanics is a strange theory. Taken at face value, the theory says that particles, such as electrons, don't have well-defined values for properties such as their position or speed, until you make a measurement. In some mysterious way that nobody understands, the particles "assume" the definite values only when you measure them.

It's nice that a sophisticated theorem that's relevant to quantum physics can be reduced to a simple colouring problem.

So perhaps the theory just isn't complete? Perhaps there is another, as yet undiscovered theory, which tells us exactly what particles are doing even when we are not watching them? The theory would have to give the same predictions as quantum mechanics for observations because those predictions have been verified in experiments more than any other theory. But unlike ordinary quantum mechanics, let's imagine our new theory does allow for particles to have definite locations, speeds and spins and so on, even when we are not trying to detect them.

This sounds like a plausible idea and indeed such theories have been developed — see here for an example. However, a result called the Kochen–Specker theorem tells us that things can't ever be as straightforward as we might hope. It says that such a new theory must be contextual. The values you measure for a particle's properties — speed, position, spin, etc — those values must somehow or sometimes depend on how you try to measure them. If this sounds confusing, then you might want to read this article to find out more about the idea of contextuality. Here we look at the Kochen-Specker theorem in more detail and even give you an idea of the proof, which is refreshingly simple.

Getting in a spin

The Kochen-Specker theorem was proved by the mathematicians Simon Kochen and Ernst Specker in 1967, so it celebrates its 50th birthday this year. "The theorem makes the idea of contextuality very vivid, without bothering your head with all these misty and controversial issues about the interpretations of quantum theory," explains Jeremy Butterfield, a philosopher of physics at the University of Cambridge. "That's because it articulates contextuality as a problem of colouring."

Elementary particles with different values of spin are represented in the work Spin Family (2009) by Julian Voss-Andreae. (CC BY-SA 3.0)

Let's start with some basics. Quantum particles have a property called spin: it's a little bit akin to what you'd think of as the "spin" of an object that is rotating on an axis, but it's more subtle than that. We don't need to go into the details here, suffice to say that when you measure the component of a particle's spin in a particular direction in space, you will only ever get one of a very limited number of values. For example, for spin 1 particles the spin can only take the values 1, −1 or 0. Quantum mechanics predicts that a spin 1 particle will have any one of these values with equal probability (i.e., the spin value will be 1 roughly a third of the time, 0 a third of the time and −1 a third of the time).

As spin 1 particles have spin of either 1, −1 or 0, the squared component of spin in any direction can only be 1 (=1² =(-1)²) or 0 (=0²). The spin in that direction is 1, −1, or 0 with probability 1/3 for each of these values. After you've squared the spin there's a 2/3 probability of the squared spin being 1, and a 1/3 probability of the squared spin being 0, because −1 and 1 have been lumped together.

Now quantum mechanics predicts a deceptively straightforward result: If you measure the squared spin of a spin 1 particle in three perpendicular directions, you will always get the answers 1, 0, 1 in some order. (Although you can't simultaneously measure the spin of a particle in different directions — they form incompatible pairs in Heisenberg's uncertainty principle — you can simultaneously measure the squared component of spin of a particle in three perpendicular directions.)

Colouring by numbers

Now here comes the colouring problem. Imagine a sphere and a triple of perpendicular axes running through its centre. Your task is to colour one of these axes red and the other two blue. But here is the catch: you need to assign the two colours to every triple of perpendicular axes in the entire sphere, but in a coherent way. Each axis must be either red or blue, but not both.

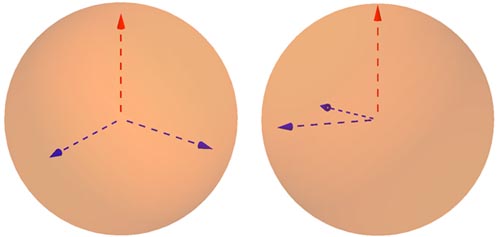
Two triples of perpendicular axes. One axis of each triple must be coloured red, the other two blue.

You can see that this is a difficult problem. Let's single out an axis that has already been coloured red, and let's assume it's the vertical one (if it isn't vertical, we simply rotate the sphere so that it is). Now every axis in the equatorial plane (and there are infinitely many of them) is perpendicular to the vertical one, and since the vertical axis is red, each of them needs to be coloured blue. "For one red I now have a vast infinity of blues," says Butterfield. "But didn't I want to have roughly a third of the sphere red and roughly two thirds blue? It looks like the blues are bound to swamp the reds when we notice that the entire equator will have to be blue."

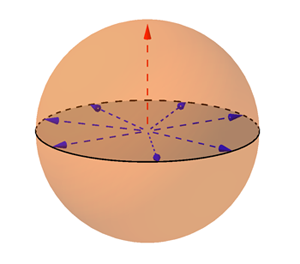
If the vertical axis is coloured red, then all axes in the equatorial plane must be coloured blue.

Kochen and Specker showed that it is indeed impossible to colour all axes either red or blue so that in every triple of perpendicular axes exactly one is red. You don't actually need to consider infinitely many axes to prove their result: a specific collection of only 33 is enough (see here for the details). When you try to colour them according to the rules, you'll eventually find an axis that needs to be painted red because it's part of a triple in which the other two are blue, but that also needs to be coloured blue because it's part of a triple in which there's already a red axis.

Context is everything

What does this mean for our measurements of spin 1 particles? Remember we are thinking of a theory in which particles have well-defined values for their spin (and therefore also for their squared spin in all directions). Let's represent the outcomes of a measurement of square spin in a triple of perpendicular directions by a triple of perpendicular axes in our sphere picture. As we mentioned above, these outcomes always give a 0 in one of the directions, and 1s in the other two direction. The 0 outcome is represented by a red axis and the other two outcomes are represented by the two blue axes in the triple.

Since we know that the colouring problem is impossible to solve, we know that there is at least one awkward axis: one that should be painted red if you consider it as part of one triple (call it triple 1), but should be painted blue if you consider it part of another triple (call it triple 2). This axis then corresponds to a direction in which the squared spin will be measured as 0 if you measure it as part of triple 1 of directions, and in which the squared spin will be measured as 1 if you measure it as part of triple 2 of directions. In other words, the value of the squared spin you see when you measure the system in the awkward direction depends on what other two directions you choose to measure squared spin in! "Kochen and Specker force on you the idea that the value you get depends on the triple, and therefore there is contextuality," says Butterfield.

You can't get away from the cold truth demonstrated by the Kochen-Specker theorem. Either you accept that a particle doesn't have a definite preset value for its spin before you measure it (that's the ordinary interpretation of quantum mechanics) or you accept that the preset value depends on what other measurements you decide to make at the same time. Both options are strange — take your pick!

About this article

Marianne Freiberger and Rachel Thomas are Editors of Plus. They interviewed Jeremy Butterfield in Cambridge in February 2017.

This article is in part based on a 2011 article by Rachel Thomas, based on an interview with the mathematician John Conway. It is part of our Who's watching? The physics of observers project, run in collaboration with FQXi. Click here to see more articles and videos about contextuality.