Benoît Mandelbrot in 2007. Image Rama.

Benoît Mandelbrot, the father of fractal geometry, died last Thursday at the age of 85. Born in Poland in 1924, Mandelbrot had dual French and American citizenship and spent most of his working life in the US. He died of cancer in a hospice in Cambridge, Massachusetts.

The Austrian painter and architect Friedensreich Hundertwasser once bemoaned what he called the "tyranny" of the straight line: "It is the line which does not exist in nature," he said and condemned any design based on straight lines as "stillborn". A bit dramatic perhaps, but he had a point that wasn't just relevant to art and design. The straight lines and perfect circles of classical geometry have given rise to centuries worth of beautiful mathematics, but there are natural forms whose intricate complexity they just cannot capture. The outlines of clouds and the intricacies of the humble broccoli are famous examples. Mandelbrot's work on fractals can be credited with bridging that gap between classical geometry and nature. And it showed that, far from being beyond the reach of mathematics, these complex forms can emerge from a few simple mathematical rules.

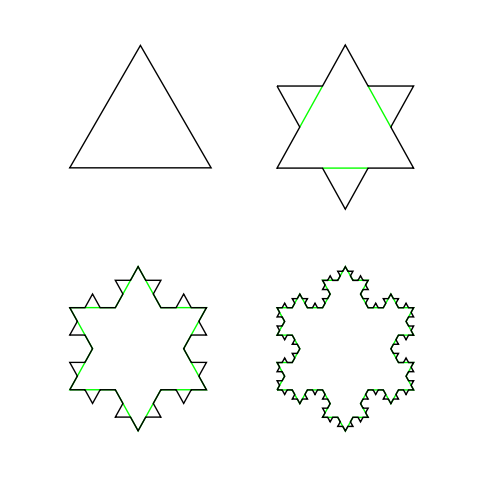
The first four steps in creating the Von Koch snowflake. Image from Wikipedia. Click here to see the snowflake emerge from an infinite number of steps.

Fractals are geometric objects that exhibit complex structure at every scale. No matter how closely you zoom in on a fractal, its complexity doesn't diminish and you often see the same structures appearing again and again. A famous example is the Von Koch snowflake. Start with an equilateral triangle and replace the middle third of each side by a "spike" consisting of two sides of a smaller equilateral triangle. Now do the same for each of the twelve straight-line segments of the resulting shape and repeat, ad infinitum. The shape you get in the end, after an infinite number of steps, exhibits the same spiky structure at every level of magnification: you'll never see a piece of straight line in its outline, because every straight-line piece that was once there has been broken up and adorned with a spike.

Mathematically, fractals live in a strange world in between dimensions. You couldn't call the Von Koch snowflake "one-dimensional" because it contains no straight lines or smooth curves at all. No amount of zooming in will reveal such one-dimensional components. On the other hand, the snowflake isn't two-dimensional either, because it occupies no area. In fact, it takes a new definition of "dimension" to sort out the snowflake's place in the dimensional hierarchy. According to this definition, the snowflake has a dimension of around 1.26. Having a fractional dimension, one that's not a whole number, is what characterises the objects Mandelbrot decided to call fractals.

Examples of fractals have been known to mathematicians for some time, the snowflake was first published in 1904 by the Swedish mathematician Helge von Koch, but they were regarded as mathematical oddities, strange constructs that had no bearing on reality. Indeed, the fractal which carries Mandelbrot's name, the famous Mandelbrot set, arose not from visual or practical considerations, but from work in pure maths carried out in the 1920s (independently) by the French mathematicians Pierre Fatou and Gaston Julia. Fatou and Julia pinned down the dynamical behaviour of a certain family of mathematical functions, but they were unable to visualise their results. Doing this would involve letting their dynamical systems run for hundreds or thousands of steps, something that's entirely impossible if you're working with pencil and paper. It was Mandelbrot's pioneering work with computers that helped reveal the magical fractal structures that emerge from Fatou and Julia's work. The most ubiquitous of them all now carries his name. (See the Plus article Unveiling the Mandelbrot set for more.)

The famous Mandelbrot set. Image Wolfgang Beyer.

Mandelbrot's greatest achievement lies in realising that fractal structures appear all over the place in real life, too. He found self-similarity in the random noise you get when transferring information between computers. The fluctuations of financial markets look similar whether you look at a graph representing a whole year, or just a week. Once his eye was sharpened, there was almost no end to the fractal patterns he spotted in nature: coast lines, galaxies, turbulence, and more. Mandelbrot capitalised on existing mathematical ideas, like that of a fractal dimension, and the power of the newly-emerging personal computers to understand, describe and produce fractals. Indeed, he created the first computer algorithm to draw the fantastical, yet life-like fractal landscapes that fractal artists have become so fond of.

Akin to the Von Koch snowflake, natural fractal structures can often be modelled by repeatedly applying a set of relatively simple mathematical rules. This doesn't only make them perfect candidates for computer exploration, but also illustrates how astonishing complexity can emerge in apparently simple mathematical or physical systems. In his work Mandelbrot made the crucial link between fractal geometry and dynamical systems, which, though governed by simple rules, can be entirely unpredictable. His book The fractal geometry of nature (1982) is a seminal work not just in geometry, but also in what has become known as chaos theory.

Zooming in on the Mandelbrot set reveals its rich structure and a tiny baby Mandelbrot set hidden inside. Image Wolfgang Beyer.

Mandelbrot's work has spawned a long legacy of practical applications. It is used to understand the fate of our Universe, of financial markets and of populations of animals and humans. In medical research it's used to shed light on the structure of our brains and our digestive system, and in developing medical imaging techniques. Fractal geometry has applications in image and video compression and even to spot art forgeries. And that's quite aside from the new world fractal geometry has opened up for artists and musicians.

But it's not just about applications. The breathtaking beauty and complexity of the fractals emerging from Fatou and Julia's work has inspired pure mathematicians to revisit the kind of dynamical systems Fatou and Julia were working on. Research over the last three decades has shed light on these intricate structures and their intimate connection to chaos and has shown that very similar fractal structures appear again and again. Foremost among them is the Mandelbrot set. Its ubiquitous nature has been explained using the mathematical rules that govern the particular mathematical universe it lives in. But, perhaps fittingly given Mandelbrot's reputation as a maverick, the exact nature of the Mandelbrot set — relating to just how crinkly its outline is — remains elusive.

Further reading

Nigel Lesmoir-Gordon has written a nice obituary of Mandelbrot for The Guardian.

See all Plus articles on fractals at a glance.