
Eat, drink and be merry: making it go down well
This article is part of a series of two articles exploring two ways in which mathematics comes into food, and especially into food safety and health. In this article we will take a dive into the rather smelly business of digesting food, and how a crazy application of chaos theory shows the best way to digest a medicinal drug. The other article explores how maths can tell us the safest way to cook food (in a microwave oven).
Making it go down well
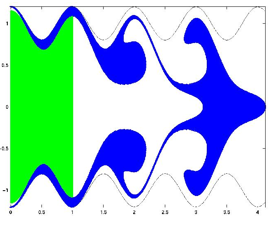
The distribution of a drug as it moves through the gut. The complex patterns of the drug as it mixes can be predicted using chaos theory.
Having eaten food we need to digest it to gain energy to live. Some foods take a long time to digest, whereas we may want to digest others more quickly. Examples of the latter type of food include "energy foods" used by athletes (and anyone else who needs energy quickly) and many types of pharmaceutical drugs. Problems with digestion lie at the heart of many medical conditions such as cholera and typhus.
The key difference between whether a medicinal drug is absorbed (and thus does some good) or "shoots straight through" is how well it is mixed up as it passes through the body. Understanding the mixing process is vital and it is here that one of the great modern developments of mathematics, chaos theory, plays an important role. Without an understanding of chaos theory we simply get the answer wrong (not just wrong but very, very, wrong).
Mathematical modelling of the digestive process not only helps understand the way that the body absorbs food, but also allows the design of more effective types of drug. Interestingly, such mathematical modelling shows that the body is cleverly designed to absorb as much food as possible, in as quick a time as possible.
When you eat food it passes down through your oesophagus, before entering the stomach. In the stomach it is broken down by hydrochloric acid to form a brown, viscous liquid called chyme. The chyme then moves into the small intestine where nutrients are absorbed through the lining of the gut wall. Finally, the waste food passes into the large intestine and then out of the body through a valve called the illeocecal sphincter. I leave it to the reader to decide for how often and how long the illeocecal sphincter is open.
To give some idea of numbers, the small intestine tightly coiled (a natural fractal) so that it is much longer than you expect given the size of the body. In fact, it is 7m long and only 1.25cm in radius. Its primary purpose is to absorb useful nutrients into the blood stream. The large intestine is 1.5m long and rather wider in diameter and is there to dispose of the waste products. Food typically stays in the digestive system for about seven hours. In particular, it stays in the small intestine, where it is absorbed, for about 4.5 hours. The small intestinal wall itself is lined with thousands of villi and microvilli and food is absorbed through these and into the blood stream. These villi form another lovely example of a natural fractal. Their existence in the gut massively increases its surface area and thus its ability to absorb food efficiently and quickly. (See the Plus article Superficiality for more on fractals and surface area.)
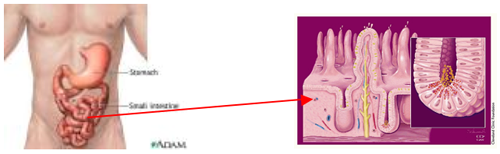
Villi and microvilli in the small intestine
What will concern us most from the view point of mathematical modelling of the food absorption is the process by which the food moves through the small intestine. There are two reasons that food moves. The first is peristaltic pumping. In this process waves are sent down the wall of the intestine and these move food along in a manner not unlike that of a surfer riding a wave on the sea. The peristaltic waves also turn out to have a major effect on the process of mixing the food in the intestine; something that was discovered as a result of the mathematical modelling which I will describe next.
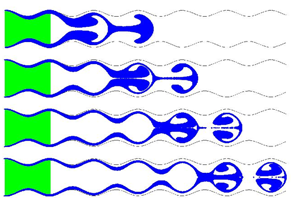
Figure 1: Food being driven by peristaltic pumping and being mixed and absorbed as it passes though the small intestine.
The second reason that food moves is due to a pressure difference between one end of the gut and the other. This pressure difference can change its direction depending upon whether the illeocecal sphincter is open or closed (think about it!) and I will return to this rather earthy calculation presently.
In figure 1 on the left we illustrate the process of a drug in moving through the gut, driven by the peristaltic waves, and also being absorbed when the illeocecal sphincter is closed. Note that when the drug enters the stomach and becomes mixed up in the chyme it forms only part of the material going through the gut. In this figure the initial distribution of the drug is shown in green and its progress in time after a few hours is shown in blue. These figures clearly show the complex shapes that the drug distribution takes as it is mixed and absorbed during its time in the gut.
Modelling the mixing process
We will now show how mathematics is used not only to predict these profiles of the food after mixing, but also to predict how well the drug is absorbed into the body. The first people on the scene of gut modelling who attempted to predict what food did as it passed through the intestine were chemical engineers. They thought that they could model the gut rather like chemicals going through a pipe. The effect of the peristalsis was considered just to be an extra driving process helping to move the food along. Whilst this gives a more or less accurate result for an average flow of the chyme (so that we know as a result how often we need to go to the loo) it tells us nothing about the way that the food mixes up in the process. To understand this vital process we need to work a bit harder and to look at the way that fluids move through narrow "pipes" such as the intestine.
Roughly speaking chyme is a slow moving and viscous (sticky) fluid. Now, a full understanding of the way that fluids move is very, very, hard (just think how hard it is to forecast the weather) and indeed a complete mathematical understanding of the nonlinear equations describing fluid motion, known as the Navier-Stokes equations, is one of the seven celebrated Clay Problems. Solve this and immortality, not to mention $1,000,000, is yours (see my Plus article How maths can make you rich and famous to find out more). However, understanding the flow of slow-moving viscous fluids is a much easier problem, especially in relatively simple geometries such as the intestine which, to a good first approximation, are long cylinders.
The key feature of intestinal flows that makes them special is the peristaltic pumping caused by the waves going along the intestinal wall. This is described by thinking of the intestine as a long cylinder of average radius $R.$ The true radius $r$ then varies with space and time as the peristaltic wave passes along it. So that if $x$ is the distance along the intestine and $t$ is time, then the radius $r(x,t)$ at point $x$ and at time $t$ is $$r(x,t) = R+a \cos{\omega(x-ct)}.$$
Here $a$ is the amplitude of the peristaltic wave, $c$ is its speed and $\omega$ is its frequency. As the chyme is very viscous, it locally sticks to the wall of the intestine, and this wave then moves it along the gut (like a surfer).
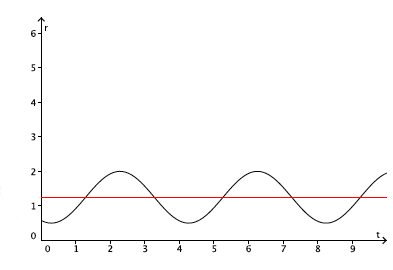
The black curve shows the radius r of the intestine at a particular point of the gut as it changes over time t for an amplitude a= 0.75cm, a frequency ω=π/8cm and a speed c= 2cm/minute. The red line shows the average radius R=1.25cm.
The velocity of the chyme is related to the pressure forcing it to flow down the intestine by a set of equations known as the Stokes equations. These look rather off-putting when written down, but for those who are interested, we have included them on a separate page. Provided that the amplitude $a$ is not too large and the wavelength of the peristaltic wave (typically about 8cm) is rather larger than the mean radius, $R$=1.25cm, of the intestine, then it is possible to solve the Stokes equations to find the velocity, and therefore the flow patterns, of the chyme.
We find that there are basically two types of flow pattern. Patterns which swirl with lots of eddies (see (a) in figure 2 below), which occur mainly when the illoececal sphincter is open, and flows with no eddies (see (b) in figure 2 below), which occur when the illececal sphincter is closed (and also in certain other pathological conditions). To visualise these we consider, as above, the flow patterns formed when we release a drug from the stomach into the chyme.
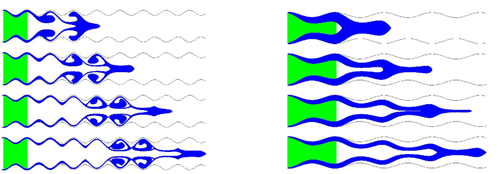
Figure 2: The left image (a) shows a flow with lots of eddies and the right image (b) shows a flow with no eddies.
The other pictures in this article show some different flow patters which arise when we change the amplitude and wavelength of the peristaltic wave. It is possible to play lots of mathematical games, looking at the different patterns of flow which occur as we change these. This gives important insights into the effects on the digestive process of various gut related problems, such as irritable bowel disorder (ISB), which helps doctors in turn to diagnose the cause of various ailments. The eddies above are due in large part to the effects of the peristaltic pumping and they play a vital role in the absorption of the nutrients and drugs which we now consider.
Modelling the absorption of the nutrients
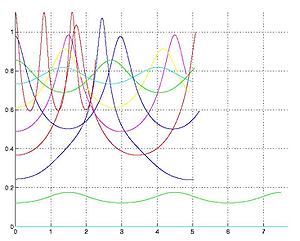
Figure 3: The paths of seven bits of the drug as they pass through the instestine.
Imagine now that you have swallowed a drug. This will be mixed up with the chyme in the stomach and will then pass into the intestine. Most of it will then move (hopefully) to the wall of the intestine where it is absorbed through the villi into the blood stream. In a worse case scenario, the drug will pass straight through the intestine without being absorbed into the blood stream. However, this is prevented by making sure that the drug is well mixed into the chyme, and thus reaches the walls of the intestine rapidly.
The importance of the eddies in the chyme is precisely that they force this mixing process. In fact what happens is that the individual parts of the drug move on chaotic paths (that is effectively random paths) as they are transported around by the eddies. Figure 3 corresponds to figure 2(a): I have plotted the paths of seven bits of the drug as the pass through the intestine. As you can see the drug is getting very well mixed, and these chaotic paths mean that the drug rapidly gets to the boundary and is absorbed.
Mathematicians call this process enhanced diffusion. It also occurs in the atmosphere and oceans when atmospheric or oceanic eddies mix up particles in the air or water.
To model this important effect we have to solve an equation which describes the way in which the concentration $c$ of the drug changes with time $t$ and space. This equation describes two processes which move the drug through the gut. One is convection by the chyme (in just the same way that moving hot air convects heat around a building). The second is diffusion of the drug, which is a random spreading, simlar to the way that smoke on a still day spreads through the atmosphere. We've included the explicit equation on a separate page.
Luckily, this equation can be solved easily on a computer to give us the concentration $c$ of the drug at time $t$. We can have a look at the results, which are of great interest to the drug manufacturers. By doing this we can play some games, and look at the effects of various pathological conditions on the gut and how these affect the absorption of the drug.
In the first picture (d) of Figure 4 below we turn off the peristaltic wave and let the chyme move through under pressure alone, taking the drug with it. This simlulates a condition in which a patient (say with IBS) has weak or irregular peristaltic pumping. In this picture red shows the main concentration of the drug, and blue a low concentration. In the second picture (e) we consider a healthy patient, and turn on the peristaltic wave. You can see that if there is no peristalitic pumping that the main concentration of the drug (the part indicated in red) is nearly all the way along the indicated part of the gut. In the case of peristalitic pumping the main concentration is about 1/3 along the gut. This means that the drug is staying in the gut for a longer period when there is peristaltic pumping than when there is no pumping. What is happening here is that the mixing due to the eddies and the resulting chaotic particle paths have meant that the drug stays in the gut much longer than if there is no mixing. Thus, much more of it gets absorbed and hopefully does us some good.
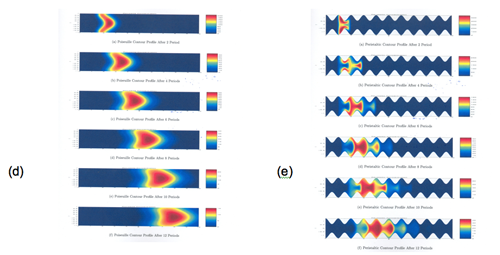
Figure 4.
We can summarise this in a graph, shown in figure 5, which is important to the manufacturers of the drug. It plots the amount of the drug that is absorbed in a particular time $t$ (in minutes) after it has been eaten. In this figure the blue curve shows the amount of drug absorbed when peristalsis is working well, and the red curve when it is not working at all.
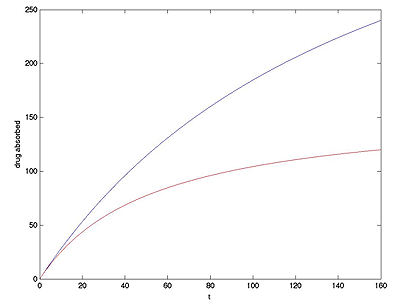
Figure 5: absorbance with and without peristalsis.
It is clear from this figure that far more of the drug is absorbed when the eddies due to the peristalsis are mixing it well. This and similar figures that we can produce by solving the equations help in both understanding the effectiveness of the drug, and also the effect of various diseases of the gut.
In this and the other article in the series, Eat, drink and be merry: making it safe, I have only scratched the surface of the many ways in which maths is used in the food industry. Other applications include the use of statistical methods to ensure food quality (indeed it was Guinness that first introduced the famous t-test in statistics), the use of imaging methods to test the freshness of products such as bread and biscuits, and the use of fluid mechanics to design many sweets. The mathematics of heat transfer is also vitally important in the design of storage and defrosting facilities for frozen food, so that the food stays fresh and therefore safe. The food industry, and especially food safety, is an area where mathematics and mathematicians can make a major contribution.
As a final thought, if you want to see how mathematics answers the vitally important question of why the large nuts in a cereal packet are always at the top, check out the Living in a complex world web-site.
About the author

Chris Budd is Professor of Applied Mathematics at the University of Bath, and Chair of Mathematics for the Royal Institution. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin.
Chris Budd is Professor of Applied Mathematics at the University of Bath, and Chair of Mathematics for the Royal Institution. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin.
Comments
Anonymous
"Finally, the waste food passes into the large intestine and then out of the body through a valve called the illeocecal sphincter."
There's some confusion and misidentification here. Contents of the small intestine pass into the large intestine through the ileocecal valve (not a sphincter), a one-way valve that prevents backflow of colonic bacteria into the small intestine. Waste exits the body through the anus, which is a sphincter.
PawanKY
Thanks for the mathematical calculation, for me it is very hard.
My elder brother is very good at mathematics but I'm too weak.
https://bakingreview.com/