
Last month David Thouless, Duncan Haldane and Michael Kosterlitz were awarded the 2016 Nobel Prize in Physics for their work using mathematical methods from topology to understand strange phenomenon in phases of matter and phase transitions. In the last article we saw how Thouless used topology to understand the quantum Hall effect. In this article, we ask mathematical physicist Fiona Burnell, from the University of Minnesota, to explain how Kosterlitz, Thouless and Haldane used topology to understand phase transitions.
Changing shape
Thouless' work on the quantum Hall effect wasn't the first time he had applied the lens of topology to understanding materials. Earlier he and Kosterlitz were responsible for changing the way we understand phase transitions and the types of materials that are possible at low temperatures. Phase transitions are sudden changes in a material's state, familiar examples are water freezing to ice or turning to steam.
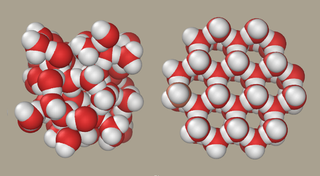
The random arrangement of liquid water molecules (on the left) compared with their ordered structure in ice.
"Before their work in the 1970s all known phase transitions were similar to ice forming," says Burnell. Phase transitions were understood in terms of a change of symmetry – for example when water changes from a liquid to solid ice. Liquid water is highly symmetrical: the molecules are arranged randomly and their arrangement would look the same if you rotated the liquid or moved all the molecules by some arbitrary distance. The highly ordered crystal structure of ice is much less symmetrical, reduced to just a few symmetries that characterise the its structure, such as rotating it by a certain number of degrees or moving the molecules by some specific distance. (You can read more in this article about symmetry breaking, and this article about symmetry in chemistry.)
Instead, Kosterlitz and Thouless discovered a topological transition between different phases: rather than understood through a change in symmetry, the transition was explained by a change in topology of the mathematical description of the quantum nature of the material. "They discovered a fundamentally new phenomenon which went between two different liquid phases," says Burnell. This fluid was confined to an extremely thin two-dimensional layer, and cooled close to absolute zero. You can picture the fluid they considered as a system of arrows lying on a plane, with the arrows free to spin around. At low temperatures if one arrow points in one direction then its neighbours are more likely to also point in the same direction.
As the system heats up, there will be excitations above this lowest energy state, where all arrows line up. These excitations come in two types. First are spin waves – if you think of the arrows as being attached to its neighbours by slinkies (the metal springs sold as toys), a spin wave is what results when you jiggle one one spin, causing propagating undulations among its neighbours. However, it was known that these spin waves were not sufficient to explain certain fundamental changes in these systems' behaviour as the temperature increased.
The second type of excitation are vortices and anti-vortices: points in space about which the direction of the arrows winds clockwise or anti-clockwise. Because of this winding, a vortex constitutes a topological change in the orientation of the arrows (relative to the configuration where they are aligned). At low temperatures these vortex-antivortex pairs are tightly bound, and only effect the direction of the arrows close by them, since on a large scale their windings cancel each other out.
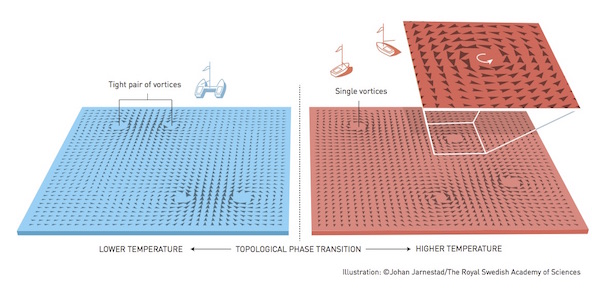
Vortex-antivortex pairs can occur at cold temperatures, but as the temperature increases these split apart as part of a topological phase transition.
Kosterlitz and Thouless showed that as temperatures increase, the vortex-antivortex pairs split and move apart so that their opposing directions no longer cancel each other out. This creates a topologically different fluid: the unbound vortex-antivortex pairs completely destroy the arrows’ alignment at long distances. This was the first time that a phase transition had been described topologically. And by showing that a phase transition could occur in such low temperatures in two-dimensional fluids, they overturned the then current theory and showed that superconductors (materials that conduct electricity with no resistance) in such systems were possible. Their theory of topological phase transitions has been used to explain phenomena in many different areas, such as condensed matter physics, atomic physics and statistical mechanics. Their work is widely regarded as one of the most important discoveries in condensed matter physics in the last century.
Strange endings
Haldane is also recognised for his work in the early 1980s on chains of atomic magnets. These atomic magnets come in two types: their spin (which you can think of as angular momentum) can take integer values (if they are bosons, such as photons) or half-integer values (if they are fermions, such as electrons). The behaviour of the one-dimensional chains are very different depending on which type of atomic magnets are involved.
Haldane discovered that an integer chain (ie one build of atomic magnets with integer spins) is gapped. This means they're in an ordered state which makes the chain "stiff": if you poke the chain, with something like a weak magnetic field, the chain will remain stiff and not respond to your prodding. Half-integer chains, however, are gapless: that is, they are not stiff at all and will respond to the magnetic field.

The winding number is a measure of how the person turns as they follow something moving along a particular curve. (Image by Jim.belk)
The difference between the behaviour of the half-integer and integer chains was due to topology, says Burnell. "What Haldane showed was that the dynamics of spin could be seen, in some sense, [in terms of] a winding number." One way to picture the winding number is to think of an arrow in three-dimensional space, that starts pointing in one direction and can rotate over time (following the wrapping process – you can read more about winding numbers in the Winding numbers or in the previous article). When the arrow comes back to its starting position the arrow head has swept out a curve on the surface of a sphere, enclosing some area. "[Haldane's work involved] understanding how the area that is swept out affects the dynamics of the whole spin chain. For an integer chain, this topological term doesn't affect the dynamics of the system. But for the half-integer chain it has an integral role, and prevents the chain from being gapped."
Haldane went on to examine integer spin chains, and to predict a very surprising new possibility in such chains: the Haldane phase. "In an ordinary gapped phase, imagine all of the spins becoming strongly paired with their neighbours in some way," says Burnell. "And if you look near the end of the chain there's nothing of interest. But the Haldane phase is another possibility. The bulk of the chain is stiff – gapped – if you apply a weak magnetic field in the middle of the chain the spins don't respond." The difference in the Haldane phase occurs at the ends of the chain: they are gapless. "If you apply the weak magnetic field at the ends, which are gapless, you get a response at the end of the chain."
This was a very controversial prediction but was soon verified experimentally. The behaviour can be explained in the way the atomic magnets interact with each other. Although the chain in the Haldane phase is made of spin 1 atomic magnets (the black ovals in the picture below), they are so strongly coupled to their neighbours you can think of each spin one piece as made of two spin 1/2 pieces (the black dots), with the neighbouring spin 1/2 pieces bonding together into pairs (the blue lines). This arangement means that for the particles at the end there is a missing partner, and you have apparently unpaired spin 1/2 pieces. "These integer spin [magnets] are very strongly coupled to each other, in such a way that they behave like a half-integer at the ends," says Burnell. If you used a high-energy microscope to just see the atomic magnets individually, the ones at the end would look the same as the ones in the middle. But zooming out, say using a low frequency magnetic field, the ends behave very differently.

A representation of the integer chain in the Haldane phase. The ovals represent the integer spin atomic magnets, which can be thought of as two half-integer spin pieces, represented by the black dots. One half-integer spin piece bonds with the closest half-integer spin piece in its neighbour, except for at the ends which are missing their partner. (Image by Milez)
Find out more about the impact of the work of Thouless, Haldane and Kosterlitz, particularly in the quest for quantum computers, in the next article...
About this article

Fiona Burnell
Fiona Burnell is currently an assistant professor of physics at the University of Minnesota, where she researches the theory of quantum materials, with a particular interest in understanding how symmetry and topology shape the types of behaviours these can have. Before joining the faculty at Minnesota she was a post-doctoral fellow at All Souls college in Oxford.
Rachel Thomas is Editor of Plus. She interviewed Burnell in October 2016, and also in July 2013 for the booklet, Mathematical physics: what is it and why do we need it? produced for the Institute of Physics. You can download a copy for yourself to find out more about the fascinating world of mathematical physics!