The EMS Prizes 2024: Richard Montgomery

Richard Montgomery has won a prestigious EMS Prize at the European Congress of Mathematics (ECM) 2024, currently taking place in Seville, Spain!

Ten of these prizes are awarded by the European Mathematical Society every four years at the ECM to mathematicians under the age of 35 in "recognition of exceptional contributions to mathematics". The winners must be of European nationality or have carried out their work in Europe. Montgomery is currently professor at the University of Warwick and did his PhD at the University of Cambridge.

Richard Montgomery has worked on objects so ubiquitous in everyday life, it's easy to forget they're mathematical: networks. We're all part of social networks in real life and online, our infrastructure is full of networks, from transport connections to the electricity grid, and there are plenty of networks within our bodies formed, for example, by the neurons in our brain. The world wide web is one absolutely gigantic network. And even the algorithms that deliver artificial intelligence can be thought of in terms of networks.

Richard Montgomery

To mathematicians a network, also called a graph, is simply a collection of nodes connected by links (called edges). The great thing about mathematical abstraction is that any network, whether biological, social, physical or virtual, can be thought of in this way – an abstract collection of nodes and links. If you can prove something about a certain type of graph, then the result will apply to any real-life network that embodies it, no matter what it is made of.

While you can understand what's going in a small graph simply by looking at it, graphs quickly become confusing as the number of nodes in them grows large. When this happens, one thing you can do is look at statistical quantities, such as averages. For example, you might look at the average number of links you need to traverse to get from one node to another. This turns out to be surprisingly small for many social networks, so you're likely to be quite closely connected to a whole bunch of famous people. A mathematical  explanation for this phenomenon (known as six degrees of separation or small worldness) was suggested in the late 1990s by Steven Strogatz and Duncan J. Watts.

Another thing you can do when a graph is large is see if you can decompose it into smaller components. For example, the London Underground map – a great instance of a graph still small enough to understand by eye – can be decomposed into smaller graphs formed by individual tube lines. It's this fact that helps us navigate London easily. Apart from some notable exceptions (eg the circle line) most tube lines (viewed as graphs)  are what mathematicians call trees. This means they contain no loops, technically called cycles.

Part of the London Underground map. See the full map here.

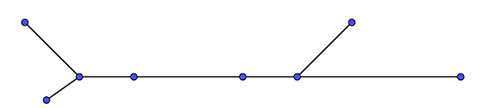
This is an example of a tree: it contains no loops (technically called cycles). A typical line on the London Underground will be a tree.

Even better, in terms of neatness, would be if a large graph could be divided up into subgraphs that are all the same: each made up of the same number of nodes connected by the same number of edges in exactly the same way. If these subgraphs were all trees, then this would be even more pleasing. Trees contain no cycles, so in a sense there's no redundancy. They are the most parsimonious graphs there are.

One of the results Montgomery succeeded in proving, to great acclaim, concerns a question of exactly this type. Imagine a graph containing some number n of nodes in which every node is connected to every other node. That's about the messiest graph you can imagine, known as the complete graph with n nodes. Back in the 1960s the German mathematician Gerhard Ringel noticed something very interesting about complete graphs with an odd number n of nodes. It appeared that such graphs could always be decomposed into copies of a tree with (n+1)/2 nodes (so that's roughly half the number of nodes of the complete graph). When put together to form the complete graph, the trees would only have nodes in common, but not overlap edges.

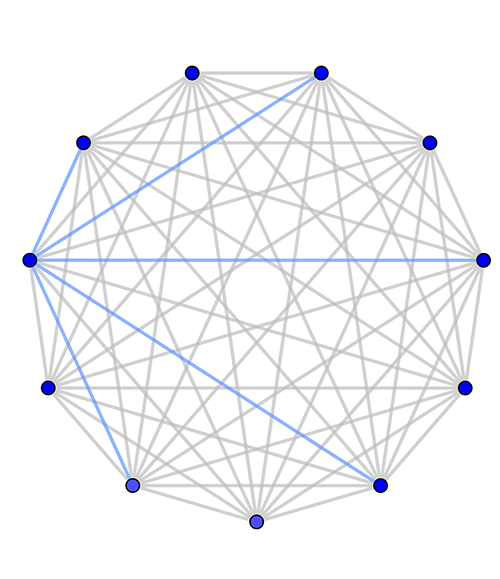
This is the complete graph of 11 nodes. The blue structure within the graph is a tree with 6 nodes. If you rotate this tree around the graph you will eventually cover all its edges, showing that the graph can be decomposed into copies of this tree.

What is more, Ringel conjectured that copies of any tree with (n+1)/2 nodes can be fitted together (without overlapping edges) to give the complete graph on n nodes. That's quite an amazing conjecture to make. If the number n is equal to 11, so you're dealing with the complete graph on 11 nodes, then the conjecture means that copies of any tree made up of 6 nodes can be arranged in such a way they give you the entire complete graph, whether it's a tree looking a bit like star or like a chain (in this we imagine a tree to be malleable as if made from rubber so we can arrange it on the plane in any way that doesn't disrupt the connectivity of the nodes).

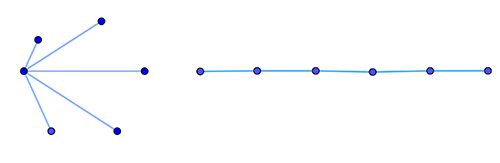
A tree shaped like a star (left) and like a chain (right). Copies of both types of tree can be put together to give you the complete graph on 11 nodes (see above). To do this you have to allow the trees to be arranged in a particular pattern, eg you might lay out the chain in more of a zig-zag fashion rather than a straight line.

Ringel's conjecture remained unproven for nearly 40 years until 2020 when Montgomery together with Alexey Pokrovskiy and Benny Sudakov finally published a proof that works for large enough n. You can read a beautiful explanation of it in Quanta Magazine.

Montgomery was awarded the Prize in front of a packed auditorium in Seville's beautiful Teatro de la Maestranza, in an opening ceremony that also featured a music by the renowned flamenco pianist Dorantes and dance. Montgomery will be giving his lecture later on in the week, and we're also hoping to snatch an interview with him for our podcast, so stay tuned!

Congratulations!

This content was produced in a collaboration with the London Mathematical Society.