Mathematicians have found a new type of pentagon you can tile the plane with. It's a nice result because pentagons are famously awkward when it comes to tiling. The most natural pentagon to think about is the regular one, whose sides all have the same length. But you won't ever get this one to tile your bathroom wall. If you try to fit several copies around a point so that they all meet at a corner, you will find that three leave a gap, and four create an overlap:

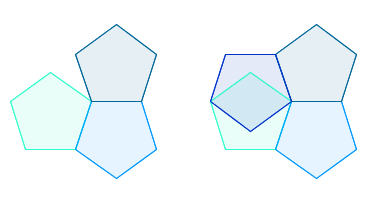
Three pentagons leave a gap (left) and four overlap (right).

And if you start with two copies offset against each other, you'll find that the gap the leave is too small to fit in another one:

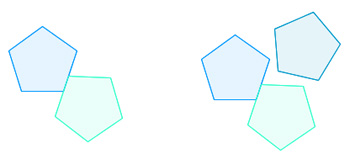
Two pentagons offset against each other (left) don't leave a big enough gap to fit in a third (right).

So there's no way to create a tiling.

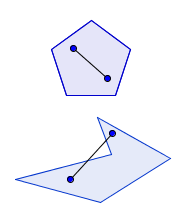
The top pentagon is convex and the bottom one isn't.

The obvious thing to do, then, is to allow the pentagon to have sides of different lengths. We won't allow it to push its corners inwards though: we only allow convex pentagons (formally, any line connecting two points in the pentagon needs to be contained within the pentagon, see the picture on the left). Are there convex, non-regular pentagons that can tile the plane?

The answer is yes, but their discovery was a painstaking process. In 1918 the German mathematician Karl Reinhardt discovered five types of convex pentagon that can tile the plane. (The pentagons that belong to a particular type all share a common feature — see this paper for a description of the types.) Then there was a slow trickle of discoveries through the century, with Rolf Stein eventually bringing the number of types up to fourteen in 1985. (You can read more about the discoveries in Alex Bellos' Guardian article.) And now, thirty years later, Casey Mann, Jennifer McLoud and David Von Derau of the University of Washington Bothell have announced that they have found another convex pentagon that can tile the plane:

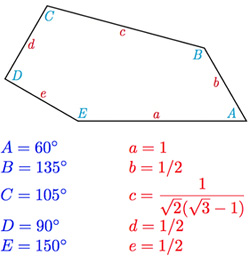
The new pentagon. Image: Casey Mann.

From each type of convex pentagon you get one particular tiling pattern. Here is a picture of them all (the new one is in the bottom right corner):

All known tilings by convex pentagons. Image: EdPeggJr.

Whether or not the latest addition is the last on the list, or whether there are perhaps infinitely many types of pentagon that tile the plane, nobody knows.

The non-convex sphinx

There are many other things you can ask about tilings, though. What if we allow non-convex pentagons, whose corners are allowed to stick inwards? In this case, you get more pentagons that tile the plane. A nice example is one called the sphinx:

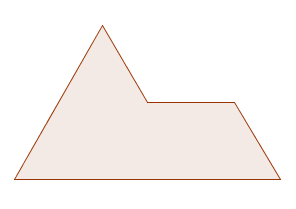
The sphinx.

If you fit two copies of the sphinx together, you get a parallelogram and it's pretty obvious that you can tile the plane with one of those:

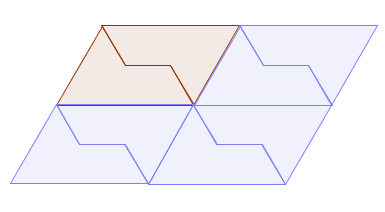
Two sphinxes form a parellelogram with which you can tile the plane.

But there's a much more exciting sphinx tiling, which looks like this:

A tiling using the sphinx.

How do you know that this really leads to a tiling of the whole plane; that is, how can you be sure you won't eventually get stuck, unable to fit the next sphinx-shaped tile? Good question, and it has an interesting answer. Notice that you can neatly fit four copies of a smaller sphinx inside a larger sphinx:

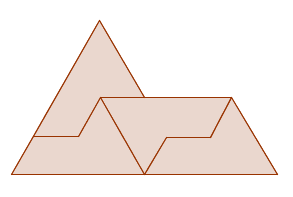
Four copies of the sphinx within the sphinx.

Now imagine blowing the picture up so that the smaller copies become the size of the larger one. Then fit four copies of the smaller sphinx into each of the four newly-blown-up copies.

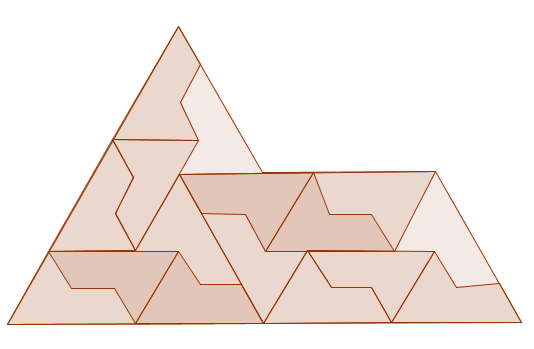
More copies of the sphinx within the sphinx.

You've now created a larger tiling of sphinxes, containing sixteen tiles. Again blow the picture up so that the sixteen smaller copies are the same size as the original copy, and fit four copies into each of those. And so on. Continuing this process, blowing up again and again, you can convince yourself that you can fill every part of the plane with same-sized sphinxes.

Another thing that's great about this sphinx tiling is that it's not periodic. The familiar tilings of the plane, say by squares or hexagons, are periodic in the sense that you could pick the whole pattern up, shift it along in a certain direction by a certain distance, then put it down again, and get exactly the same picture as before. That's not the case for a tiling by the sphinx (formally, a sphinx tiling is aperiodic). You simply can't shift the pattern along in a way that ends up with a perfect fit between the new and the old picture. Aperiodic tilings have fascinated mathematicians for a long time (see this article) and have even led to a Nobel Prize in Chemistry (see this article).

When five won't fit

The five-pointed star has five-fold symmetry.

All this was about shapes with five sides, but there is also another direction to move in once you have realised that a regular pentagon won't tile the plane. Rather than asking "are there any other five-sided shapes that do?" you can ask "are there any other shapes with five-fold symmetry that do"? The regular pentagon has five-fold symmetry because you can rotate it around its centre point through a fifth of a full circle (72 degrees) and it'll look exactly the same as before. There are other shapes that have the same rotational symmetry, an example is the regular, five-pointed star.

So can you tile the plane with shapes that have five-fold symmetry? The answer is that nobody knows: it's an unsolved problem in maths (you can find out more in this article). In terms of tilings, the number five remains trouble.