Folding fractions

Rachel Thomas
Submitted by Rachel on March 2, 2015

Can you fold a piece of paper in half? Of course you can, it’s easy, you just match the two corners along one side. But can you fold it in thirds? You might be able to fold it into thirds with a bit of fiddling and guessing, but what about into fifths? Or sevenths? Or thirteenths? Here is a simple way you can fold a piece of paper into any fraction you would like – exactly – no guessing or fiddling needed!

Folding a third

To start, take a square piece of paper and mark half way along top side with a small crease. Now fold the bottom left corner to meet this halfway mark and crease the paper.

Mark half way
Fold bottom corner to middle of top side

The first thing to notice is an interesting relationship between the three triangles you've created, one on the top-left, one on the top-right, and one on the bottom-left overhanging the side of the paper.

We've folded three similar triangles

At the centre of the top edge three angles fit together to make 180 degrees. One of these is a right angle (marked with a square corner in the picture), which means that the pair of other angles (marked with the single and double lines in the picture) add to 90 degrees. Each of the angles of this pair also form part of a right-angled triangle (the top-right and top-left triangles), which means the other angle of the pair also appears in each of these right-angled triangles. And the bottom-right triangle also shares an angle with the top-right triangle. And, as it is also a right-angled triangle, it too contains the same pair of angles.

This all means that the three triangles are similar – they have the same shape. That is to say, they all have the same angles, and so, have the same ratios of lengths of their sides. We can use these similar triangles, along with Pythagoras' theorem, to fold the paper in thirds.

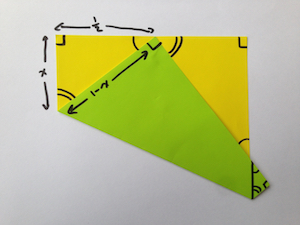
We've folded three similar triangles

If we take the length of the side of our square paper to be 1, our top left triangle has one side of length $1/2$, one side of unknown length which we'll call $x$, giving the other side a length of $1-x$. Then, by Pythagoras' theorem, we know that

  \[ x^2+\left(\frac{1}{2}\right)^2 = (1-x)^2. \]    
Expanding this out:
  \[ x^2+\frac{1}{4}=1-2x+x^2 \]    
which, by rearranging, gives us $x=3/8$.

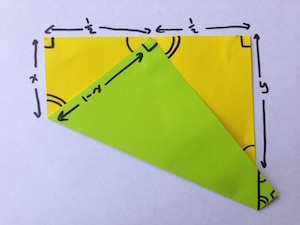
Finding the length of the sides of the top-right triangle

We can now calculate the length of the sides in the top-right triangle. This triangle has one side of length $1/2$ and another side of unknown length $y$. Because the triangles are similar we know that the ratio of the lengths of their sides must be the same. So

  \[ \frac{y}{\frac{1}{2}} = \frac{\frac{1}{2}}{x}. \]    
And as $x=3/8$, we find that $y=2/3$. So we can construct $1/3$ by folding this length $y$ in half.

Folding a third

Folding any fraction

Kazuo Haga, a retired professor of biology from Japan, came up with this ingenious method. Although a biologist, he was very interested in using origami to explore mathematics (you can find our more in his fascinating book). In fact, Haga realised that this method was even more useful.

Suppose instead of folding your bottom left corner of the paper to some point halfway along the top edge, you instead fold the bottom left corner to a point a distance of $k$ along the top edge.

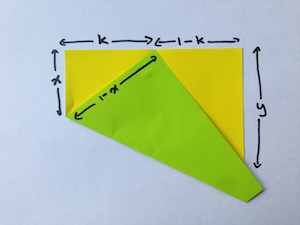
Folding any fraction

Then, the top-left triangle has sides of length $k$, $x$ and $1-x$. Then, as above, Pythagoras' theorem tells us that:

  \[ x^2+k^2=(1-x)^2 \]    
which rearranged gives $x=(1-k^2)/2$. And by the similar triangles argument we have that
  \[ \frac{y}{1-k}=\frac{k}{x}. \]    
If we put these two equations together we find
  \[ \frac{y}{1-k}=\frac{k}{(1-k^2)/2} \]    
which can be rearranged as
  \[ y=\frac{2(1-k)k}{1-k^2}. \]    
And (since $1-k^2=(1-k)(1+k)$) this can be simplified to
  \[ \frac{y}{2}=\frac{k}{1+k}. \]    
This is known as Haga’s Theorem and it allows us to fold any fraction we would like from a square piece of paper.

Folding a half
Folding a third

We've already seen $k=1/2$ allowed us to fold $1/3$. What if we rotate the square paper and fold the bottom left corner up to a point $1/3$ along the top edge? Then we have $k=1/3$ in Haga's Theorem which means that

  \[ \frac{y}{2}= \frac{1/3}{4/3}=1/4. \]    

Starting from a third
Folding a quarter

So far, starting from 1/2, we've used Haga's method to fold 1/3 and then 1/4. And if we carry on repeating this method we can fold any fraction. If we start with $k$ being some number $1/N$, then

  \[ \frac{y}{2}=\frac{1/N}{1+1/N}=\frac{1}{N+1}. \]    
So by repeating Haga’s method over and over, we can construct every unit fraction (one with 1 in the numerator): folding 1/5....

Starting from 1/4
Folding 1/5

... folding 1/6....

Starting from 1/5
Folding a 1/6

...folding 1/7...

Starting from 1/6
Folding 1/7

...and so on. And then we can use these to create any multiple of these unit fractions, and so fold any rational number. Hooray for Haga!

About the author

Rachel Thomas is Editor of Plus.

About this article

This article was inspired by content on our sister site Wild Maths, which encourages students to explore maths beyond the classroom and designed to nurture mathematical creativity. The site is aimed at 7 to 16 year-olds, but open to all. It provides games, investigations, stories and spaces to explore, where discoveries are to be made. Some have starting points, some a big question and others offer you a free space to investigate.

Comments

Submitted by Anonymous on March 4, 2015

Very cool. Interesting that you can trisect a side, but this does *not* allow you to trisect an angle (i.e., fold a 30 degree angle at the corner) since this would require you to divide a side by 1/sqrt{3} which, alas, is *not* rational.

Submitted by Anonymous on March 9, 2015

You can trisect an angle with folding. But you can't do so with a compass and ruler. See trisect angle

Submitted by Anonymous on March 9, 2015

It's true you can't trisect an angle with a compass and ruler. But you can trisect an angle with folding/origami.

Submitted by Anonymous on March 5, 2015

The link for Haga's book is broken

Submitted by Marianne on March 9, 2015

Thanks for spotting that, we have fixed it.

Submitted by Anonymous on April 2, 2015

Lovely idea .. just that in practice it's usually an A4 piece of paper that needs folding into thirds to fit in an envelope ... can anyone improve on this idea for this context?

Submitted by Jon on September 5, 2016

Haga's method is great for squares, but you're right, it won't work very well for an A4 (or any rectangle) sheet. You will need to look at the crossing diagonals method for that. Fold one crease diagonally across the A4 sheet, and one line diagonally from one corner to halfway down the edge, and they will intersect at the 1/3 point.

Submitted by Fu Wei on July 18, 2019

I have summerized 16 methods for trisecting A4 Paper:
https://www.flickr.com/photos/119967028@N08/48308136022/in/dateposted-public/

Submitted by Anonymous on April 2, 2015

It is a nice article.

Haga's theorem are there,
http://www.origami.gr.jp/Archives/People/CAGE_/divide/02-e.html
Mathematics of paper folding,
http://en.wikipedia.org/wiki/Mathematics_of_paper_folding#cite_note-12

Haga's book, we can get by Amazon,
ORIGAMICS: MATHEMATICAL EXPOLORATIONS THROUGH PAPER FOLDING

Submitted by Anonymous on April 28, 2015

It is not as elegant as the intercept theorem, thousands of years ago.

https://www.flickr.com/photos/129045076@N07/16394585596/in/set-72157650598443945

Submitted by Anonymous on June 10, 2015

Please provide more information for the sections of which you work the equations out. I am still stuck on how you converted X^2+1/2^2=(1-X)^2 into X^2+1/4=1-2X+X^2. Please provide the answer to that equation in a comment or edit the page to include more information. Thanks :)

Submitted by Marianne on June 10, 2015

You simply multiply out the brackets on each side of the equation: (1/2)^2=1/4 and (1-x)^2 = 1-2x+x^2.

Submitted by Anonymous on May 31, 2016

This was really easy to follow for someone who knows how to do stuff with equations. It was really helpful and it looks like it took a while to make so thanks for putting in the effort.

Submitted by Hiroshi Okumura on December 25, 2017

A generalization of Haga's fold and several new theorems can be seen in the paper "Haga's theorems in paper folding and related theorems in Wasan geometry Part 1". The paper can be dowload at http://sangaku-journal.eu/.

Submitted by Hiroshi Okumura on December 27, 2017

The relationship between the two fractions can be obtained from
Theorem 3.1 in the paper. Thank you very much.

Submitted by George Plousos on June 7, 2020

The same folding of the square has two more interesting properties. I have made their interactive constructions below (are activated by double clicking).

A famous result from Japan (1893)
https://www.geogebra.org/m/P8JF3mHB

Solution to the problem of doubling the cube
https://www.geogebra.org/m/hdEMmBWY