
Friends and strangers
In 1928, Frank Ramsey was wrestling with a problem in mathematical logic. To solve it, it seemed to him, he needed to show that the mathematical systems he was studying would always have a certain amount of order in them. At first sight, the systems were free to be as disorderly as they liked, but Ramsey thought that even in the most unruly, the sheer size of the system should force parts of it to exhibit some kind of order.
In proving that his intuition was correct he invented a new branch of mathematics, which is now known as Ramsey Theory. He read the resulting paper to the London Mathematical Society, but died, at the age of 26, before it was published in their Proceedings.
Ramsey Theory still has applications in the study of logic. But it is also a very attractive subject in itself, since its basic ideas can be understood very easily, and involve drawing colourful pictures. On the other hand, it's also an active research area, since it raises some spectacularly difficult questions. When the last round of Fields Medals were announced in 1998 - the Fields is mathematics' most prestigious award, its nearest equivalent to a Nobel prize - one of them went to the British mathematician Tim Gowers, in part for his work in Ramsey theory. In this article we'll see that Ramsey Theory has the ability to ask even very simple-looking questions which have defied all attempts to answer them so far.
Order from chaos
The fundamental kind of question Ramsey theory asks is: can one always find order in chaos? If so, how much? Just how large a slice of chaos do we need to be sure to find a particular amount of order in it? (Incidentally, when talk about "chaos" in this article we just mean something disordered or jumbled. There's no connection with the technical meaning of "chaos" in mathematics, which is to do with dynamical systems.)
That sounds like an odd question, here is a concrete example. Suppose there is a room with six people in it. We are interested in whether people in this room know each other or not. Let's call two people friends if they know each other, strangers if they don't.
We're looking for examples of order, and clearly the most orderly case would be if the six are either all friends, or all strangers. Unfortunately the people have been chosen at random, so there will probably be a jumble of friends and strangers in the room. Suppose we draw lines joining every pair of people in the room and colour them blue if the two are friends, red if they are strangers. Then the result might look something like this:
![[IMAGE: Coloured K6]](/issue16/features/ramsey/images/K6.gif)
This picture - mathematicians call it a graph - looks totally chaotic. We certainly don't have six friends or six strangers! But we can still ask: can we at least find three people in the room, who are either all friends or all strangers? Put another way, can we find a blue triangle (three friends), or a red triangle (three strangers)?
In this case the answer is "yes". Charlie, Evelyn and Fred are all strangers to each other. But what if the original graph had been different? Would we always have been able to find an orderly set of three people, given by a monochromatic triangle (all one colour, from the Greek monos, "single", and chroma, "colour"),?
Experimenting with some paper and coloured pencils will soon convince you that, with six people, there is always a monochromatic triangle. But how would we prove this is true? One way would be simply to list all possible colourings, and check each one in turn. Unfortunately there are over 30,000 possible colourings, so this proof would be more than a little tedious.
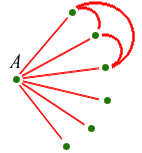
Luckily it turns out that we can prove it much more easily. First we choose any point, and note that five lines come out of it - one to each of the other five points:
![[IMAGE: 5 lines from a point]](/issue16/features/ramsey/images/5edges.gif)
With five lines, there must be at least three of one colour - at least three red lines or at least three blue lines. Let's suppose there are three red lines (if there were three blue lines instead, the argument would be exactly the same but with "red" and "blue" swapped). So we have four points like this:
![[IMAGE: 3 red edges]](/issue16/features/ramsey/images/3rededges.gif)
What colours are the three remaining lines? Well, if even one of them is red, then it makes a red triangle together with point A (left). And if not, the three together make a blue triangle (right):
![[IMAGE: 3 red edges]](/issue16/features/ramsey/images/3rededgestri.gif) |
![[IMAGE: 3 red edges with blue triangle]](/issue16/features/ramsey/images/3rededgesbluetri.gif) |
Either way, we have our monochromatic triangle.
Would 5 points be enough?
We've proved that with six points (or more, of course), there must always be a monochromatic triangle - in other words that with six people or more, there must be three friends or three strangers.
This suggests the question, "How many people do we need, to be sure of finding either three friends, or three strangers?" This is our first example of a Ramsey number, and is written as R(3,3). We've seen that six people is certainly enough; in other words, R(3,3) isn't any larger than 6. But would five points have been enough - in other words, is it the case that any group of five people will have either three friends or three strangers? The graph below with five points shows that the answer is no, since it has no monochromatic triangle:
![[IMAGE: Graph for 5 people]](/issue16/features/ramsey/images/pentagram.gif)
This shows that R(3,3) cannot be less than 6. Taking these two results together proves that R(3,3)=6.
Looking for more order
Now that we have understood what a Ramsey number is, we can try to find other examples. For example, R(5,5) would tell us how many people are needed to be sure of finding either five mutual friends or five mutual strangers. Of course, we don't yet know that there is always an answer: perhaps no amount of people will guarantee, say, 10 friends or 10 strangers. (In fact we'll prove at the end of this article that there always is an answer, even though we usually don't know what it is!)
To make sure you've followed thus far, you might like to consider the following two questions:
- What is R(2,5)?
- If we know R(a,b), what can we say about R(b,a)?
Check the answers before reading on.
Now let's be more ambitious: we want to find four people who are either all friends or all strangers. In our brand-new notation, we want to find R(4,4). For the moment, though, this is too hard, so we'll content ourselves with something a little easier, namely finding R(3,4).
Finding R(3,4)
How many points do we need, to guarantee that we can find either three points all connected by blue lines, orfour points all connected by red lines - in other words, one of the following?
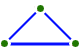 |
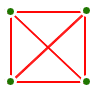 |
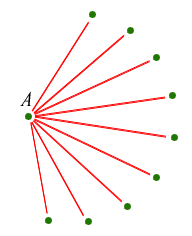
Firstly, we claim that 10 points is certainly enough. Let's try to prove this. Suppose we have 10 points, joined with red and blue lines in the usual way. Choose a point, and note that 9 lines come out of it.
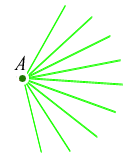
There must either be at least 6 red ones, or at least 4 blue ones (otherwise there won't be 9 in all!) So we are in one of these two possibilities (I'll only draw the lines we're interested in):
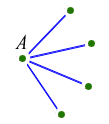 Case (i) |
 Case (ii) |
Let's look at case (i) first. What colour are the lines in (i) other than the blue ones shown? If even one of them is blue, we have a blue triangle, in other words three friends (left); if not, they are all red and we have four strangers (right). Either way we are done:
 |
 |
So now let's look at case (ii). There are 6 points (besides A) there. And we have already discovered that R(3,3)=6, so of these 6 points, 3 must form either a blue triangle or a red triangle, putting us in one of these two cases:
 |
 |
In the case on the left we have our three friends, and in the case on the right our four strangers. So once more we are done.
This argument has put a bound on R(3,4): we know it exists and it cannot be more than 10. But it could still be less than 10. In fact, by a cunning variation on the argument above, we can show that 9 points will do.
Eight points aren't enough
On the other hand, 8 points would not be enough, as the following diagram shows. (All the blue lines are shown; all the remaining lines are assumed to be red.) No 3 points form a blue triangle, and no 4 points are all connected with red lines.

So now we know that R(3,4)=9. Also, as we saw earlier, we can exchange the places of "red" and "blue", so the same argument shows that R(4,3)=9.
Finding R(4,4)
Now we can use this knowledge to find R(4,4). First, we claim that 18 people is enough to guarantee either four friends or four strangers. The method of proof should begin to look familiar by now. Say we have a graph with 18 points, and lines between them coloured blue or red. Take one point. 17 lines come out of it, so at least 9 of them must be one colour - red, say:
We already know that R(4,3)=9, so among those 9 points there must be either four friends - in which case we're done - or three strangers. In the latter case, since all three are strangers to A, we have four strangers including A. So we have either four friends or four strangers, which is just what we claimed.
Once again, we have found a bound: R(4,4) certainly exists and it is at most 18. This time, by luck, the bound happens to be the best possible: 17 points aren't enough to guarantee a monochromatic set of four points. To show this, we need to find a graph with 17 points with no such monochromatic set! This has been done, and you can see a beautiful construction of such a graph on a separate page.
As a result we know that R(4,4)=18.
Bigger Ramsey numbers
With a bit of work, we were able to find R(4,4) exactly. But proving it existed was not so hard. The final step showed that we could put a bound on R(4,4) as long as we had bounds for R(3,4) and R(4,3). These also broke down into simpler steps: we can bound R(3,4) as long as we can bound R(3,3) and R(2,4), and so on. In mathematical notation, we know that R(a,b) exists as long as R(a-1,b) and R(a,b-1) both exist.
Also we've already seen that R(a,2) and R(2,a) always exist (they're simply equal to a). So to show that, for instance, R(5,5) exists will break down into a series of steps, as in the diagram:
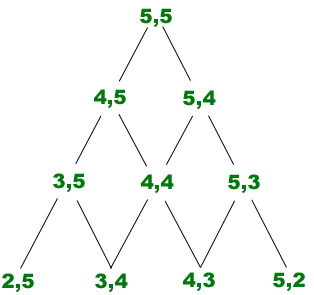
Each case breaks down into the two cases below it, and we've already done the cases in the bottom row. So R(5,5) certainly exists, and similarly for R(6,6) or for that matter any R(a,b). This is Ramsey's Theorem, and it tells us that however much orderliness we want, we can find it as long as the graph we are given is big enough.
However, it's important to remember that this method doesn't find the exact Ramsey numbers for us, even though it enables us to find bounds.
Nobody knows
So what is the true value of R(5,5)? The answer is: nobody knows! In fact, very few Ramsey R(a,b) numbers are known (with a and b both bigger than 2). We've already seen that R(3,3)=6, R(4,3)=9 and R(4,4)=18. Besides this only three more values are known: R(5,3)=14, R(6,3)=18 and R(7,3)=23. The most we can say about R(5,5) with our present knowledge is that it is somewhere between 42 and 55.
How can it be so difficult to get an accurate value? Arguments like the ones I've used in this article allow us to find upper bounds on the Ramsey numbers we're interested in - for example, we saw quite easily that R(4,3) could not be bigger than 10. But to show that it could not be as small as 8, we had to construct explicitly a graph with 8 points, as a counterexample. The problem is that we are looking for examples of order, so the best counterexamples will usually have lots of disorder - they will look random. This makes it hard or impossible to find a "rule" that gives good counterexamples. Anything constructed by rule will probably have too much order in it.
Also, our upper bounds may be too high, but how will we ever prove it? Perhaps by examining all the possibilities on a computer? But a simple example will show this will never work. Say we wanted to show that R(5,5) is at most 54 - in other words, to show that 54 points will always guarantee the existence of 5 points all connected together by lines of one colour. We would have to look at all the possible ways of colouring lines between 54 points either red or blue.
How many ways are there? First we need to know the number of lines, which, by a well-known formula, is
(54 × 53) / 2 = 1431.
Each line can be coloured either red or blue, so the number of possible colourings is
2 × 2 × 2 × ... × 2,
where the number of 2's multiplied together is 1431 - in mathematical notation this is 21431 or over 10400. This number is far, far bigger than the number of particles in the known Universe (about 1080). So there is no chance of even the fastest computer imaginable ever finishing such a search. This is a puzzle we may never know the answer to.
About the author
Imre Leader is a fellow of Trinity College, Cambridge and a lecturer in the Department of Pure Mathematics and Mathematical Statistics, Cambridge University.
Comments
richarmartini
thank you very much for the explanation it was very iluminating for me (in the books of graph theory never is so clear as you.. )
Anonymous
I am finishing my master degree and I´m writing about Ramsey´s Theorem.
I´m from IMPA (National Institute of Pure and Applied Mathematics), Rio de Janeiro, Brasil.
Excelent article. I´ll recommend to my friends.
If you have something more, please e-mail to pcesar26@gmail.com.
Thank you very much.
Paulo Cesar S. Jr.
Anonymous
I am a high school student who is working on Ramsey Theory as my Mathematics Project.
This site is wonderful in explaining concepts and illustrating examples.
I am wondering what are some of the simple application of Ramsey Theory in real life that I could investigate on?
Anonymous
I do not get it... R(3,3) is 6 so R(3,4) should also be 6 for you are looking for a triangle OR an interconnecting square.
And because this symetry-thinghy it should apply also to R(4,3) here it is the use of OR.
Another thing is "eight points aren't enough" if you look at the setup then every even number would behave the same so with some level of confidence you could also say "32 points aren,t enough" which is obviously not the case.
Yorge
Think about it this way: a graph whose edges have been painted with red and blue and where the ONLY clique you find is in red cannot satisfy both R(3,4) and R(4,3), which we know it must.
Anonymous
I am writing a paper on Ramsey Theory and found this article very helpful. How can I cite this article?
Anonymous
Wonderful write-up. Thank you for teaching me something new
Harsha
This is an awesome article and the one of the best articles on The Party Problem or Friends and Strangers that i've ever read.
And I loved the simulation in which we can try out combinations
Really loved it!!!
Kenna
I'm a bit confused regarding your proof for R(4,4). Supposing 3 strangers, they are strangers amongst themselves not strangers to A. All of those vertices are actually still friends with A under our initial assumption. I know R(4,4) is 18 but I'm not sure your proof is correct.
Wil Ransome
Just read this and much enjoyed. I couldn't see much about Frank Ramsey himself. People may not know that he was the brother of Michael Ramsey, who was Archbishop of Canterbury from 1961 to 1964. Somewhere you may well mention this but i can't find it.