Happy birthday Quicksort: Starting with bubbles

When you are buying online you usually get the option to see the items you searched for ordered by price, average customer rating, or perhaps date. If you have ever tried to put a bunch of things (e.g. books on your shelf) in order, you'll know it takes time. This is why the world owes a huge debt of gratitude to computer scientist Tony Hoare for inventing Quicksort — a famous sorting algorithm which celebrates its 60th birthday this year.

Tony Hoare, the inventor of Quicksort, in 2011. Photo: Rama, CC BY-SA 2.0 FR

Hoare developed Quicksort long before online shopping had even been conceived of, but it's still hailed as one of the best sorting algorithms and implemented in many programming languages and libraries. Its anniversary is being celebrated at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge this month, and it's at the INI that we (virtually) met Hoare to ask him about his most famous brain child. Its invention, Hoare told us, started on a couch in a room at Moscow State University where he was a student visitor, studying under the eminent mathematician Andrey Kolmogorov.

"I had received a letter from the National Physical Laboratory offering me a job working on machine translation of languages," says Hoare. "[It was using] the Ace computer that Alan Turing had designed, which excited me a lot. So I spent some time thinking about machine translation."

To translate a sentence from one language to another you have to look each word up in a dictionary. Back then, this involved a dictionary stored in alphabetical order on magnetic tape. To look up a word on this memory device you had to first move through all the words thay come before it. This meant that any method for translating a sentence would have to start with putting the words in that sentence in aphabetical order so you could look them up as quickly as possible.

"I'd been on a Mercury Autocode course in the previous year, [while I was] studying statistics at Oxford, so I thought why I don't sit down and program [an algorithm for doing that]?", says Hoare.

Bubble sort

The first thing that emerged from the train of thought started on the couch, Hoare says, was not Quicksort, but another algorithm called bubble sort.

The idea behind bubble sort is simple: given a list of things (e.g. numbers) that need to be put into an order (e.g. increasing) you first compare the first two elements and swap them if they are not in the correct order. In the list you now have, you then look at the second thing and the third thing and swap them if they are in the wrong order. You keep going with the pair of things at the third and fourth place in the list, the fourth and fifth place in the list, etc, until you have reached the end of your list. If during this process you didn't have to swap any things at all, then this means the list was already in the correct order, so you stop. If you did have to swap at least one pair, then you start the same process again from the beginning of the list, comparing pairs of consecutive things. Eventually, after doing this a number of times, your list will be sorted. Here's an example:

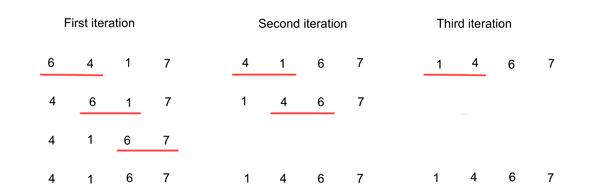
Bubble sort in action, sorting the list 6, 4, 1, 7 into ascending order. At each step, the numbers underlined in red are compared and swapped if they are in the wrong order. The reason that each iteration contains one less comparison than the previous one is that we know that the numbers 7 and 6 were put in their correct place at the first and second iteration respectively, so we can ignore them in subsequent iterations (see here to find out why). Note that after the second iteration the list is already correctly sorted, but the algorithm doesn't know this yet. It needs an entire run through the list without any swaps to know that it is finished, hence the third iteration.

Bubble sort gets its name from the fact that the things in your list will gradually move towards their correct place, just like bubbles rise to the surface. But simple as it is, it's not the most efficient way of sorting a list. Just how many steps (i.e. comparisons and potential swaps) you have to make before the entire list is sorted obviously depends on how ordered the list was to start with. It's possible to show that in the worst case scenario you (or rather the computer implementing the algorithm) would need to perform $n(n-1)/2$ steps to sort the entire list of length $n$ . (See here to find out why this is true.)

The reason this is bad is that $n(n-1)/2$ grows large quite quickly with $n$ . For a list of fifty things ( $n=50$ ) the worst case scenario would require $(50 \times 49)/2=1225$ steps, for a list of a hundred things ( $n=100$ ) it would require $(100 \times 99)/2=4950$ steps, and for a list of 150 things ( $n=150$ ) it would require a frightening $(150 \times 149)/2=11175$ steps.

Note that if you multiply out the bracket in $n(n-1)/2$ you get

$\frac{n(n-1)}{2}=\frac{1}{2}n^2-\frac{1}{2}n.$

As $n$ grows large, the $n^2$ term in this expression becomes dominant. When quantifying the run time of algorithms (measured by the number of steps needed) computer scientists focus only on such dominant terms, which is why bubble sort is said to have a worst case running time of $O(n^2)$ . (You can find out more about how to quantify the run time of algorithms here. )

If you're an optimist, you won't judge an algorithm by its worst case performance, of course, but sadly things don't get any better for bubble sort when you consider the average running time, that is, the result you get when you average the running time over all possible initial orders of the $n$ things. You are still stuck with $O(n^2)$ .

With bubble sort not quite as satisfactory as it could be, Hoare decided to think again, and the result was Quicksort. To understand the workings of this clever algorithm, see the next article.

About this article

Marianne Freiberger is Editor of Plus. She talked to Tony Hoare in May 2021 when Hoare was taking part in the Verified software: From theory to practice workshop run by the Isaac Newton Institute. See here for other articles based on this interview.

This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.