Happy birthday Quicksort!

Next month sees the 60th birthday of Quicksort, a sorting algorithm that even at its advanced age is still hailed as one of the best. In the previous article Quicksort's inventor, Tony Hoare, told us how his famous brain child was preceded by something called bubble sort. We now go on to explore Quicksort itself. It's not as simple as bubble sort, but the idea is beautifully elegant.

Let's assume from now on that the list of things that need to be put into order are numbers that need to be arranged in ascending order (the algorithm works the same for any other list of object and orderings). Given such a list of numbers, you first choose a pivot number in your list. It's against this number that you compare all other numbers in the list.

As an example, let's choose the pivot to be the first number in the list. The overall idea is to now check through all the remaining numbers and move them before the pivot if they are smaller than the pivot. The pivot number is now in its correct position in the list: all the numbers that are smaller than it come before it and all the numbers that are larger come after it. Here is an example:

As our example indicates, it may be that the other numbers are not yet in the correct order. If this is the case, you simply apply the same process to the smaller part of the list and larger part of the list separately: you pick the first number in each list as the pivot and partition each list into a smaller and larger part. You carry on like this until at your last iteration all the sub-lists contained either one or no number at all. When this has happened your list is sorted.

The question now is, how exactly do you do the partitioning of the list into numbers that are smaller than the pivot and numbers that are larger? You could just define two new lists, one called SMALLER and one called LARGER, and then sort numbers into SMALLER and LARGER as appropriate. For a computer this means defining extra data structures (two new lists at each round of the overall process) which in turn means using more memory. It would be better to avoid this by doing the partitioning in a way that doesn't need extra lists.

Hoare thought up an ingenious way of doing just that. Imagine again a list of numbers with the first position chosen as the pivot. Now imagine putting your left index finger on the number to the right of the pivot (the second number), and your right index finger on the last number. The aim is to find pairs of numbers that are in the wrong order (with respect to the pivot) and swap them, by scanning the list both from the left and from the right.

Your left index finger goes first. It checks whether the number it is pointing at is smaller than or greater than the pivot. If it is smaller, you move your left index finger one position to the right, if it is greater, you leave your finger where it is. Once your left index finger has stopped (in a position with a number that's greater than the pivot), your right finger starts. It checks whether the number it is pointing at is smaller than or greater than the pivot. If it is greater, you move your right index finger one position to the left, if it is smaller, you leave your finger where it is. Once both your fingers have stopped, you have identified two numbers that are in the wrong order with respect to the pivot, so you swap them around. Here's an example:

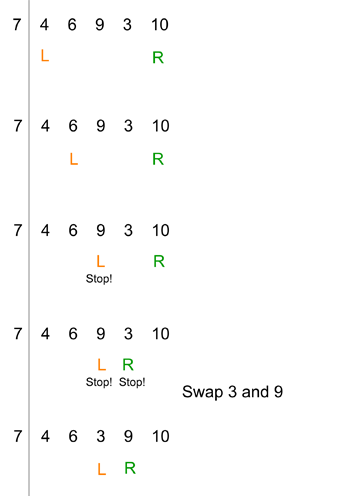
Afterwards, if your two fingers haven't crossed (so your left finger is still left of the right one) you start the whole process again, with your left finger going first as before. After some number of repetitions of this process, when both fingers have stopped, they will have crossed. In this case, you don't swap the numbers in their respective positions. The locations of your fingers indicate the divide you were looking for: all the numbers to the left of your right finger are smaller than the pivot and all the numbers to the right of your left finger are larger than the pivot. Here's our example continued:

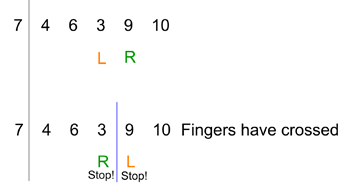
This process can quite easily be programmed on a computer. We now have an algorithm that sorts a list by partitioning smaller and smaller sub-lists (see above) and an algorithm for doing the partitioning at each iteration, so overall, we have an algorithm that sorts the list: that's Quicksort. We should note that the algorithm as we described it can get into trouble when the pivot happens to be smallest or largest number in the list, but there are ways to deal with that, see Wikipedia for the details.

We should also note that this isn't the only way of performing Quicksort. Firstly, the pivot does not necessarily have to be the first number in the list. We could also have chosen the last one, or one somewhere in the middle, or even chosen the pivot at random on every iteration. There are also other ways of performing the partioning (for example the Lomuto partitioning scheme). So really, Quicksort is a family of algorithms that all proceed according to the same scheme overall, but whose details can vary. Each is an example of a divide and conquer algorithm which recursively breaks the problem to be solved down into smaller chunks.

How quick is Quicksort?

As we said in the previous article , the number of steps the algorithm has to perform before it's finished depends on how the list was ordered originally. But just as for bubble sort, it's possible to work out the worst case and average case performances. When it comes to worst case, Quicksort is still as bad as bubble sort, giving $O(n^2)$. On average, though, Quicksort performs better, giving $O(nlog(n))$. You can see in the graphs below that $n^2$ grows quicker with $n$ than $nlog(n)$. This means that as your list gets longer, the average case performance of Quicksort gets increasingly quicker than the average case performance of bubble sort.

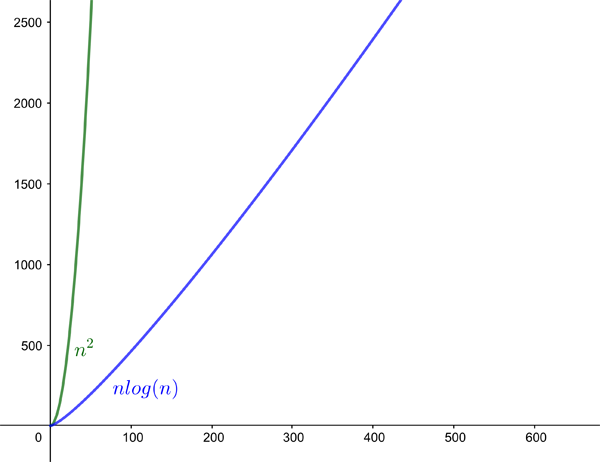
The graphs of n² (green) and nlogn (blue). They illustrate that the Quicksort algorithm is increasingly faster on average than bubble sort as your list gets longer.

The exact number of steps needed by the algorithm also depends on which variant you use (remember we are really talking about a family of algorithms). In practice, you can try and exploit this variety to choose the variant that best suits the kind of data you are trying to sort. Overall, though, the results for worst and average case performances still hold. You can find out more about the runtime of various Quicksort variants on HappyCoders.

Hoare published his description of Quicksort in July 1961 when he was 27 years old. The clever algorithm proved a door-opener to the world of research where Hoare went on to make many other important contributions.

"[Quicksort] has become a textbook example of divide and conquer, recursion, and sorting," he says. "[To pursue] an academic career without a doctorate, which is what I had to do, inventing Quicksort was a very good alternative!"

Hoare has enjoyed a long and prosperous career working in both in academia and in industry. You can find out more about some aspects of Hoare's work in the next article: Beyond Quicksort

About this article

Marianne Freiberger is Editor of Plus. She talked to Tony Hoare in May 2021 when Hoare was taking part in the Verified software: From theory to practice workshop run by the Isaac Newton Institute. See here for other articles based on this interview.

This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.