
A (hi)story of geometry
One of the neatest rules you learn about geometry at school is that the angles of a triangle always add up to 180 degrees. But despite what your teacher told you this is not always true! It took mathematicians centuries to understand why. And, as we found at a recent event, the history of geometry shows how developments in mathematics have fundamentally changed the way we think about the world around us.
The troublesome parallel postulate
Officially the story of geometry begins with the mathematician Euclid who lived in Egypt around 300 BC. Euclid wrote The Elements, a book which gave a set of five rules (which mathematicians callaxioms) on which he thought all of geometry should be built. These were statements that were so obvious that everyone should be able to just accept them as true with no further justification needed. (You can find an easy introduction to his axioms here.)
The rule that the angles of a triangle always add to 180 degrees is a version of Euclid's fifth axiom. Euclid's original version was a little more complicated:
If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
This is illustrated in the image below. In the image the two lines meet a third line forming two angles that are less than 90 degrees each, which means, in Euclid's flat geometry, they meet.

If the two lines failed to behave like this, if they didn’t meet, then they would be parallel. Euclid’s fifth axiom tells us that two lines are parallel if they each meet a third line at right angles, and this is why it is also called the parallel postulate. With a bit of extra work you can show that it is equivalent to saying that the angles in a triangle add up to 180 degrees, at least as long as you are working on the flat plane.
While this parallel postulate was incredibly useful, it also was very troublesome for mathematicians. "It caused a lot of problems," said Jeremy Gray, a historian of mathematics who was speaking at a recent satellite event at the London Mathematical Society as part of the Modern History of Mathematics research programmeat the Isaac Newton Institute for Mathematical Sciences. While the postulate said that two non-parallel lines would meet, that meeting point might be very far away – even light years away! "It's hard to speak with confidence of an intersection point that might be billions of miles away!"
The parallel postulate didn't seem to be as obvious as Euclid's other four axioms. Compared to the other four axioms, which contained simple statements such as “a straight line can be drawn through any two points”, the fifth seemed way too complicated. This led many to believe that we should be able to deduce it from the others – to show that if the first four axioms hold then the fifth automatically holds as well. "People wanted to delete the parallel postulate and instead prove it from the other four axioms," said Gray. And so over the centuries many mathematicians tried to do just that. And they all failed.
The answer is beneath you
The parallel postulate can't be deduced from Euclid's other four axioms because it isn't always true. There are situations where the first four axioms hold, but the parallel postulate doesn't.
This is because Euclid described his rules of geometry in terms of points and lines on a flat plane. And this is in stark contrast to the ground we actually stand on, which is only approximately flat. We live on the roughly spherical surface of the Earth and here Euclidean geometry doesn’t work. The first four axioms hold, but the parallel postulate doesn't.
Imagine you are standing on the equator between two lines of longitude. The three lines you are looking at, the equator and the two longitudinal lines, are examples of great circles: they wrap around the fattest part of the Earth, achieving a maximal diameter – no other circle drawn on the surface of the Earth can be bigger. Great circles also give you paths of shortest distance: the shortest route between any two points on the Earth is along the unique great circle that contains them both. Great circles are to spherical geometry what straight lines are to Euclidean geometry: they are paths of shortest distance (called geodesics) and they should therefore obey the same laws.
But here is the surprise: if you measure the angle each line of longitude makes with the equator, you will find that both angles are right angles. Yet, like all lines of longitude, these intersect at the North and South poles: they are not parallel. What we have here is a surprisingly familiar counterexample to the parallel postulate.
A triangle on the sphere is formed by arcs of great circles. But it bulges outwards and its angles add up to more than 180 degrees. How much more depends on the size of the triangle: the sum of the angles in a small triangle will only be a whisker above 180 degrees because for small regions the surface is approximately flat. But as your triangle gets larger and larger – say a triangle connecting London in the UK, Münster in Germany and Perth in Australia – the sum of the angles increases.
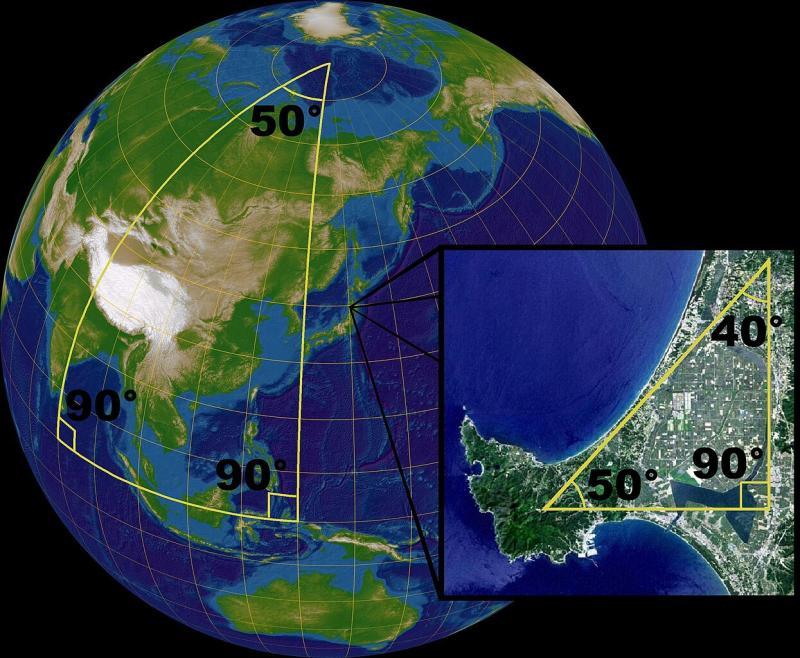
The mismatch between spherical and Euclidean geometry becomes particularly apparent when you look at maps which are, after all, attempts to depict a sphere on a flat piece of paper. Any flat map of the Earth is distorted in some way. The most commonly used, called the Mercator projection, is fairly accurate around the equator but grossly exaggerates the distances and sizes as you get nearer the two poles. Greenland seems vastly larger than Africa when in reality it is around 14 times smaller. (You can read more in our introduction to map projections.)
A struggle against the darkness
Once you get used to it, spherical geometry is still pretty natural: you can visualise it, you can draw diagrams of it, and if all else fails you can draw pictures on an orange. But there is another type of geometry, hyperbolic geometry, that is much more exotic.
Gray used this story to illustrate some of the insights that can be learned from the history of mathematics and the way it can be used to understand the mathematics taught and researched today. As well as humanising the subject, and making mathematics more inclusive with examples of work from around the world, the history of mathematics also helps us understand the context and priorities of the maths and science we study today. "The history of maths makes properly researched connections to other things, like physics, or even literature," said Gray. "And the history of recent maths can help our ideas about the direction and priorities of maths today."
The history of geometry is a perfect example of how over the centuries our changing mathematical understanding directly impacted the direction of science and the way we understand the world around us.
Gray continued the story of hyperbolic geometry with mathematicians János Bolyai, in Hungary, and Nikolai Lobachevskii, in Russia. In the 19th century Bolayi and Lobachevskii joined the struggle to make sense of the parallel postulate. And a struggle it was, as Gray demonstrated with the kind of heady, romantic writing from that era from Bolyai, Lobachevskii and their contemporaries.
For example Farkas Bolyai, János' father and fellow mathematician, wrote about the parallel postulate in letters to his son:
"It is unbelievable that this stubborn darkness, this eternal eclipse, this flaw in geometry, this eternal cloud on virgin truth can be endured."
And in a paper Lobachevskii deplored how far geometry was behind other areas of mathematics:
"Nothing in mathematics begins in such darkness as Euclid's opening remarks and has such a shameful lack of rigour as one encounters in the theory of parallels."
Bolyai and Lobachevskii both tried to rectify this lack of rigour. They, like so many before them, set out to prove the parallel postulate from Euclid's other axioms. To do this, they assumed the parallel postulate to be false and hoped to find that the resulting geometry would be paradoxical and impossible, thereby proving wrong the assumption that the postulate was false. A classical example of proof by contradiction, or reductio ad absurdum.
But the geometry that did result was not paradoxical. What Bolyai and Lobachevskii had discovered, each independently, is now called hyperbolic geometry. The first four axioms that hold in Euclidean and spherical geometry also hold for hyperbolic geometry, but in this strange new world the angles in a triangle add up to less than 180 degrees.
Strange new worlds
So what does a surface that exhibits this strange hyperbolic geometry look like? It is hard to visualise. But try thinking of a kale leaf which gets more and more crinkly towards the edge. To get from a point A to a point B a little bug living on the leaf has to climb over all those crinkles, preferably along a path of shortest distance (the geodesic again).
Now imagine flattening the kale leaf, hopefully without squashing the bug, and smoothing it out flat. The paths of shortest distance on the leaf do not necessarily turn into straight lines on the flattened version of the leaf. Instead, they may turn into different types of curves. This is very similar to the way that straight lines of the shortest paths around the Earth, great circles, turn into curves on any flat map.

If you flatten a crinkly hyperbolic surface that is tiled with identical triangles you get something like the image above, where it is flattened into a disc. The straight lines (or geodesics) of the hyperbolic surface become curves on the flat disc.
We can also see the identical triangles from hyperbolic space are distorted in the flat disc, becoming more and more squeezed as you move towards the boundary of the disc. "Remember the distortions in the maps of the world," said Gray. "This is a hyperbolic tiling. The triangles are the same size, but appear to be getting smaller in this flat disc."
When we flattened the spherical geometry of the Earth into a flat map, we didn't have "enough" material – we had to stretch out some areas of the spherical Earth on the flat map. But for hyperbolic surfaces, like our imaginary kale leaf, we have too much material! When we flatten a hyperbolic space some of the regions are distorted and squeezed to appear smaller on the flat map.
So far we have looked at hyperbolic surfaces, two-dimensional spaces with hyperbolic geometry. But there is a similar model for three dimensional hyperbolic geometry and even for dimensions beyond that. No wonder that Bolyai exclaimed in a letter to his father:
“I have discovered things so wonderful that I was astounded... From out of nothing I have created a strange new world.”
Decades later it became clear that hyperbolic geometry is not just a fanciful dream: it is exactly what Einstein needed in 1905 for his special theory of relativity. Gray explained that our evolving understanding of geometry directly impacted our understanding of the nature of the world around us. Over the centuries mathematicians took us from thinking intuitively in terms of flat Euclidean geometry, to the spherical geometry of the planet we live on. "And, in a long and winding route, to Einstein's general theory of relativity and the start of modern cosmology."
The work by Gray and his colleagues on the history of mathematics illuminates not only the development of the subject of mathematics, but also the central role it plays in human culture. "Maths is not just another subject," said Gray. "Maths affects the way people think about the physical world they inhabit, and how they talk about it."
About this article
This article is partly based on a talk by Jeremy Gray at History of mathematics for mathematical leadership, an event held at the London Mathematical Society as part of the Modern History of Mathematics research programmeat the Isaac Newton Institute for Mathematical Sciences.
Jeremy Gray is a mathematician, from the University of Warwick and The Open University, researching the history of mathematics.
Rachel Thomas and Marianne Freiberger are the Editors of Plus.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
