
Hitting the spot

There'll be plenty of penalties at Euro 2016.
Euro 2016 is up and running. By 22 June, 24 teams playing in six groups will have completed 36 matches in total. During the group stages accumulated points (three for a win, one for a draw) will decide which 16 teams go forward to the knock-out rounds. For the group games the odd draw is not especially critical, but at the knock-out stage, matches that remain tied after extra time will be decided by the dreaded penalty shootout. How confident players feel in this trial of nerve and skill depends very greatly on which team they play for; Germany have an 83% success rate in Euro and World Cup shootouts whereas England, very much the stragglers, have won only 17% of their encounters.
Is there such a thing as a perfect penalty kick? Before answering this question it's useful to look at some broad statistics to help shape an approach to a possible solution.
Zones and envelopes
Some years ago a colleague and I set out to determine just how much of the goal area could be covered by a goalkeeper diving in attempting to save a penalty. This led to the concept of the diving envelope, the goalkeeper's maximum reach in a finger-tip save (see the figure below). This leaves an attractive, technically unprotected area of the goal, which we dubbed the unsaveable zone. The zone is about 30% of the goal area, a target easily attained under normal playing conditions. Of course nothing is normal in shootouts and even the most accomplished professionals succumb to nerves on really big occasions.
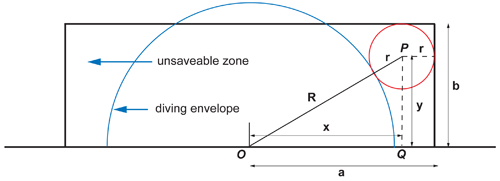
Geometry for optimum location of shot.
Nevertheless, our concept of the envelope and the zone were largely borne out by studies of successful penalty kicks in major competitions. About 50% of shots played inside the envelope are saved, whereas those targeted on the zone give a success rate of over 80%. Hit the ball within the goalie's technical reach and you'll succeed only 50% of the time; you might as well spin a coin rather than take a shot. Aim at the zone, however, and you are highly likely to get your name on the score sheet.
So placement beats "hit and hope" every time; but is there a perfect spot, a "zone within the zone" so to speak? Let's see how a little algebra and geometry can help to answer this question.
Things to avoid in a penalty kick
It's easily seen in the figure above that the zone progressively widens as we move the aiming point from the bottom corners of the goal to the top. Choosing the bottom corners is not a good strategy; not just because the zone is narrower here but because it's easy to scuff the ball along the ground when shooting low. This reduces its speed and returns a little advantage to the goalie. So aim high, keeping the ball as far as possible from the diving envelope, the crossbar and the goal post. In other words aim for the centre of a circle which just touches all three; this is shown as point $P$ in the figure above.
Finding the centre, $P(x,y)$ is not difficult. With the notation of the figure above we see that \begin{equation}x^2+y^2 = (R+r)^2.\end{equation} But $x=a-r$ and $y=b-r.$ Substituting these values into equation (1) we find after a little tidying up, \begin{equation}r^2-2r(a+b+R)+a^2+b^2-R^2=0.\end{equation} To solve this quadratic equation we use the radius of the diving envelope, $R= 2.85 m.$ The goal half-width is $a=3.66 m$ and the post height $b=2.44 m.$ This gives the radius of our aiming circle as $r = 0.65 m.$ The circle is drawn to scale in our figure above and it follows that our target point is $0.65 m$ from both the crossbar and the goalpost or equivalently, $3.01 m $ from the goal's centre and $1.79 m$ above the ground. Are these values any use at all to players whose turn to take a penalty in the shootout has arrived? Emphatically not! Quadratic equations should be the last thing on a player's mind when he or she steps up to the penalty spot. Intense focus on the aiming point is the overriding requirement and fortunately there's a better way to visualise the target in practice.In the figure below we see a goalkeeper standing at arm's length from the goalpost. Perfect placement using the values we've calculated turns out to be just to the right of the goalie's head — and please note that female goalies are also very tall in the elite game nowadays, so our aiming point is gender-neutral! How many penalty takers at Euro 2016 will adopt this strategy? I'll be keeping a tally throughout the competition, but perhaps some budding statistician would like to work out the success rates for top and bottom corner shots and report back to Plus.
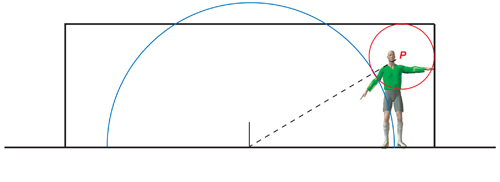
Aim at P, just right of the goalie's head!
Postscript
Having completed the analysis a nagging thought occurs. Astute readers will point out that quadratics have two solutions, and I've chosen the value of $r$ from equation (2) that fits the scaled geometry of the first figure beautifully. What about the other solution? The two values of $r$ that satisfy the equation are $r = 0.65 m$ and $r = 17.24 m$ and a glance at the figure below shows that the circle with the latter radius, like the smaller one, touches the diving envelope (extended) and the post and crossbar (both extended). In other words it's a perfectly valid mathematical solution, but one which we reject on physical inspection.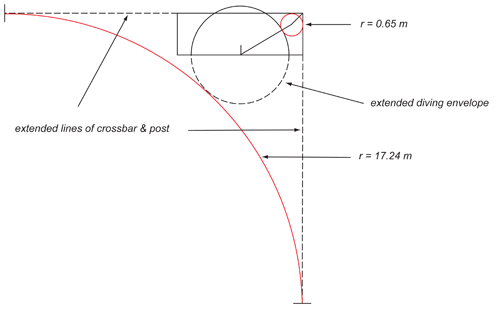
Illustrating both solutions of the quadratic equation.
But wait a moment ... suppose England's dire record in shootouts is because they've chosen the wrong solution to the quadratic! There might just be time before the knock-out rounds start to contact their training camp in Chantilly, just north of Paris. It's worth a shot.
About the author

Ken Bray is a theoretical physicist and a Senior Visiting Fellow at the University of Bath, UK. He has made a special study of the mathematics of football and the factors affecting the ball's flight, and has lectured, broadcast and published widely for both academic and general audiences. He has gone on record as saying that as much as 30% of a footballer's technique is down to an intuitive understanding of maths and science (although they shouldn't go anywhere near a computer!). His book How to score: Science and the beautiful game has been reviewed in Plus.