We were very sad to hear of John Conway's death on April 11, 2020. He's been a hero of ours for a long time, as he was to many mathematically curious people. Instead of writing a comprehensive account of his life and mathematical accomplishments (you can find examples from Princeton University and Scientific American), we thought we'd reflect on the thoughts he shared with us over two interviews, and the experience of meeting him as a person, as well as a mathematician.

We were lucky enough to interview Conway in our early days on Plus in 2002, and again in 2011. We say we interviewed him, but as we've mentioned elsewhere, the experience of interviewing Conway was more a case of sitting back, holding on tight and enjoying the ride. He spoke non-stop in a great wave of mathematics and philosophy and anecdotes, until he was finished, and he went, and we were left with reams of notes and hours of recordings to try to work into a finished piece.

Life...

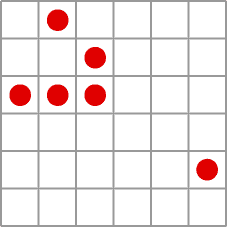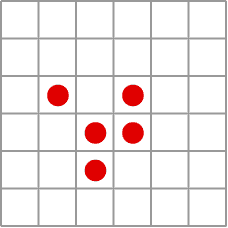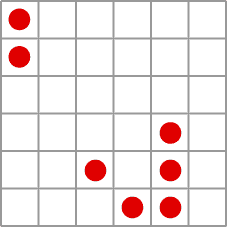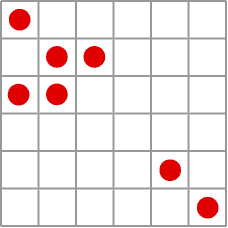
Gliders walking across the plane

After learning about Conway in group theory courses at university, and then regularly glimpsing his skill at bringing simplicity, beauty and humour to his mathematical research over the years, we were definitely a little star struck when we first met him in 2002. He told us about the system he called Life, probably the achievement he is mostly widely known for outside of mathematics. Conway had been trying to find a universal system — a sort of infinitely programmable computer — and developed Life over two years of coffee breaks with a group of graduate students using a go board.

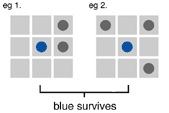
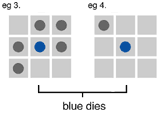
Life is played out on an infinite board of cells arranged in a grid. You start the system off by populating the board with some configuration of live cells. Then each cell either is born, or dies, according to a small set of rule (see box). From these simple instructions an astonishingly life-like array of phenomena emerge, such as glider guns that produce a steady stream of gliders that walk off across the board til they meet and interact with other populated regions of the board. This glider gun was the final piece necessary for Life to be a universal system, adding to all the various configurations of live and dead cells that were necessary for arbitrary computations. (You can read more here.)

Rules to live by... Life is played on a grid of squares where each cell is either alive (occupied) or dead (empty). You start with an initial configuration of live cells, and the game progresses through generations as the life and death rules are applied. A live cell survives to the next generation if it has two or three neighbours. A live cell dies if it has four or more neighbours (overcrowding) or if it has only one neighbour or none (isolation). A dead cell becomes a live cell in the next generation if it has exactly three neighbours (birth).

Conway went on to explain that although imitating life wasn't really the goal, in a way, finding artificial life was. "I believe that if you have a large enough configuration you will see evolution in the plane," Conway told us. "What would happen is every now and then there would be a creature capable of reproducing itself and then they would start to populate the plane. Except the plane is still filled with random junk which might kill some of them. So some of them will be better equipped to survive than others and every now and then they will run into something that hurts and might start a change. Most of these changes will probably be for the worse but every now and then one of these might be for the better and then you know the story. You will probably get evolution happening and you would get creatures that really deserve the name living." He could even imagine that if Life was left to play for a very long time, these creatures might eventually achieve consciousness.

You can explore the Game of Life in the interactivity below, created by our amazing colleague Oscar Gillespie. It starts off with a random pattern of live cells. If you would instead like to choose your own starting arrangement of live cells, click Clear the grid and then click on the individual cells you would like to be live. To run just a single step of the Game of Life, click on Run a generation. To run through many steps, click Run. And to start again, click Stop and then Reset.

For some very interesting starting patterns, see the article Cellular automata.

The Universe...

We were very pleased to have the opportunity to interview Conway again in 2011. During his visit to Cambridge he was to give a lecture, which, as was his common practice, had to be advertised with no abstract. He told us he didn't like to be constrained by deciding his lectures in advance — what if he didn't feel like talking about the pre-decided topic on the day in question?

In this interview we asked Conway to retrace his steps with friend Simon Kochen as they created the most controversial theorem of their careers: the Free Will Theorem. This theorem essentially says that if we, humans, have free will, then so do quantum particles. Free will in humans had already been the subject of debate for philosophers, mathematicians and scientists for centuries, so it's hardly surprising that giving a similar property to subatomic matter was going to cause controversy. But Conway and Kochen's arguments are compelling when you follow their reasoning from the standpoint of quantum physics.

The story begins with Einstein's distress at uncovering the cloudy and fitful nature of quantum reality. Quantum physics went against the deterministic nature of the scientific theories that had gone before it, including Einstein's own special and general theories of relativity. Properties of quantum particles, such as position and momentum, do not have a fixed, definite value before they are measured; rather the probabilistic nature of quantum physics means that these observations can have a range of values and this value is only fixed when a measurement is made. (You can read more in our ridiculously short introduction to some very basic quantum mechanics.)

Conway was working with Kochen on trying to understand how Kochen's previous result — the Kochen-Specker theorem — related to the difficulties Einstein had uncovered in quantum physics. The Kochen-Specker theorem showed that a certain property of quantum particles (called squared spin, which is measured in different directions) cannot possibly have a fixed predetermined value for every possible direction.

"This reminds me of when I was a little boy and I played Twenty Questions with my two sisters," Conway told us. Many of us have played this game. You decide on an object and say whether you're thinking of an animal, vegetable or mineral. Then the other players ask you questions that have only two possible answers: yes or no.

"But I used to do the following. If I sensed somehow that my two sisters were getting too close to my object I would choose a new object! But you have to be quite clever to do that because you have given answers that applied to your old object. (By the way, the penalty of being caught out was to have your earlobes bitten! My god it hurts like hell! I can still remember it 65 years later!) You have to find a new object that gave those various answers too." For Conway this childhood memory was a metaphor for what was going on in quantum physics. (You can find out more about the Free Will theorem in this article.)

Everything...

Conway had had a stroke in 2006 and, although fit enough to travel and lecture to packed out audiences, he still felt its effects. When we interviewed him in 2011 he said: "In my present condition I keep thinking of death all the time, it's a damn nuisance." Despite this, our discussion of the free will theorem led him to many musings on the beauty and mysteries of life, the universe and everything.

Simon Kochen and John Conway explaining their Free Will Theorem (photo: Princeton University, Office of Communications, Denise Applewhite)

The Free Will Theorem is based on three axioms, which, while some are unproven, are experimentally verified. Therefore many mathematicians and physicists believe the consequences of these, as described by the Free Will Theorem, will be true, despite the philosophically challenging nature of the result. The theorem has also had a profound impact on Conway himself. "It's really affected how I look at the world. I believe that the glimmerings of freedom are in every particle — in the clouds, in everything — the particles are all taking free decisions."

Conway likened his perception of the free will of particles to looking at the trees in California and Mexico that temporarily become home for hundreds of thousands of migrating monarch butterflies each winter. "When you see it from a distance, at a large scale, you can't see the individual flutterings." But as you look closer it becomes a mass butterflies. "That's what I believe this table is. If you could look at it much expanded the particles would all be fluttering, taking free decisions that don't globally affect the thing very much."

Conway readily acceded that this might seem whimsical or far-fetched. "I can't prove this nonsense, but there's no reason to disbelieve it!" And he immediately emphasised he wasn't not attributing some sort of consciousness to the particles. "You mustn't misread it, we're not asserting these particles make decisions, we're not saying they have any consciousness. What happens is they act, they indubitably act, and which action the particle does is free in this sense, it is not a predetermined function of the past. And that's not the same as randomness, oh dear me no!"

And mathematics

John Conway

We'd like to leave you with Conway's explanation of what has been one of the great attractions of doing mathematics. The advantage of mathematics, he told us in 2002, is that it does not require expensive equipment to make discoveries. The mind alone is all that is required to study mathematics. As Conway said, he could "interrogate the abstract universe from an armchair, bath or bed!" And, more than this, the mathematical universe is not just parochial to him. "Though I can sit alone and interrogate that abstract universe, it is not just my universe. It is my colleagues' universe as well. There is a certain stability about it, and I actually believe it is the Martians' abstract universe as well.

"I have always been interested in the abstract world. And the reason is that I don't understand why it's there. I don't understand why theorems don't change. We can still prove Pythagoras's theorem, it's still there 2,000 years after it was found."

The achievement Conway is proudest of is his discovery of a new class of numbers, the surreal numbers, and it gives him pleasure to think that they will remain in this abstract universe for millennia, just like the theorems of Pythagoras (Donald Knuth wrote an excellent introduction to surreal numbers in the form of a short story — Surreal numbers: How two ex-students turned on to pure mathematics and found total happiness).

"I think that the Martians have also discovered the surreal numbers somewhere, perhaps not in this galaxy... In that case we would have achieved some sort of intellectual connection. [The alien mathematician would be] the Martian John Conway!"

About the author

Rachel Thomas is Editor of Plus.