Mathematical mysteries: Goldbach revisited

Since we first wrote about the Goldbach conjecture (see Mathematical mysteries: the Goldbach conjecture), we have had many requests for more information about it, and about how our Goldbach calculator works. We can answer some of your questions here but the Goldbach conjecture touches on a strange area of maths that may leave you even more curious than before...

To recap, Goldbach started this quest in a letter to Euler in 1742. The conjecture we know today is not the one he first proposed though Euler showed it to be equivalent. In his letter, Goldbach made the following assertion:

Every whole number greater than 5 can be written as the sum of three primes.

Clearly the first few cases are easy to write down:

• 6 = 2+2+2
• 7 = 2+2+3
• 8 = 2+3+3

We can break down this assertion into two separate assertions as follows:

1. Every even number greater than 4 is the sum of three primes
2. Every odd number greater than 5 is the sum of three primes

Let's look at (1) more closely. To add three numbers and get an even number requires either 3 even numbers to start with or two odd numbers and an even number. However, there is only one even prime: 2. Therefore, (1) is just the same as saying that every even number greater than 2 is the sum of two primes.

(2) is even simpler. If we have an odd number greater than 5 we can always subtract 3 (a prime) and get an even number greater than 2. (1) says that this number must be the sum of two primes so, adding our 3 back again gives three primes that sum to our odd number.

We can now state the problem in its more usual form:

Every even number greater than 2 is the sum of two primes.

It is suggested that although Euler simplified Goldbach's conjecture he didn't see it as worth spending time proving.

This issue's mystery

Here is another unproved statement about primes that is very similar to the Goldbach conjecture:

Every even number can be expressed as the difference of two primes.

At first sight, it looks very similar to the Goldbach conjecture but there is an important difference. To find out why you'll need to know a little more about how our Goldbach calculator works.

Inside the Goldbach calculator

Some readers have asked us how the Goldbach calculator published in Issue 2 works.

The procedure or algorithm used by the calculator is described below:

Given an even number: n, find all prime pairs p1+p2 = n.

The algorithm is divided into two halves. Firstly we create a list of all primes from 2 up to n. Secondly we search this list exhaustively to find all the prime pairs.

Finding primes

To list all the primes up to n we use a method known as "the sieve of Eratosthenes". This method is best visualized by drawing a square grid with at least n boxes and numbering them starting with 1 in the top-left corner and working down to the bottom-right corner. The idea is to mark (say be colouring in) all the boxes which belong to non-primes. To do this proceed as follows:

1. Mark the box number 1, which is not prime by definition.
2. Set p to 2.
3. Starting from box number p, count p boxes forward and mark the box you stop on, then count p boxes forward again and mark again. Repeat this process until you run out of boxes.
4. Starting from box p again, scan forward until you get to the next unmarked box. Change the value of p to the number in this box and return to (3).

The clever twist to this method is that in (4), once you've used all the unmarked boxes in the first row of your grid you're done! The boxes left unmarked in the grid are the prime numbers.

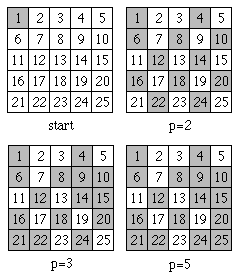
The sieve of Eratosthenes applied to a simple 5x5 grid.

Finding prime pairs

Once we have a list of primes, we can find the prime pairs as follows:

1. Set p1 to the first (smallest) prime in the list.
2. Set p2 to the last (largest) prime in the list.
3. If p1>p2 we're done.
4. If p1+p2<n then set p1 to the next prime in the list and return to (3).
5. If p1+p2>n then set p2 to the previous prime in the list and return to (3).
6. Otherwise p1+p2 must equal n. Record this prime pair. Set p1 to the next prime in the list and p2 to the previous prime in the list and return to (3).

Finding prime triples

The method above extends easily to find the prime triples for a number n as follows:

1. Set p1 to the first (smallest) prime in the list.
2. Set p2 to p1.
3. Set p3 to the last (largest) prime in the list.
4. If p2>p3 set p1 to the next prime in the list and return to (2).
5. If p1+p2+p3<n then set p2 to the next prime in the list and return to (4).
6. If p1+p2+p3>n then set p3 to the previous prime in the list and return to (4).
7. Otherwise p1+p2+p3 must equal n. Record this prime triple. Set p2 to the next prime in the list and p3 to the previous prime in the list and return to (4).

The above procedure terminates when we run out of primes for p1 in (4).

The mystery deepens

Does our algorithm for finding the Goldbach triples always stop? Yes it does. For each value of n we're given we build a finite list of primes and scan this list to find the pairs/triples that sum to it.

In principle, even if we removed the constraint on the size of the number entered our program would always take a finite number of steps. It doesn't matter if the Goldbach conjecture is true or not. If we stumbled upon a number which could not be broken down into the sum of three primes our program would simply terminate without having printed out any triples but still in a finite number of steps.

Now let's look again at this issue's mystery. Namely that every even number, n, can be expressed as the difference of two primes. Clearly there could be many possible pairs that have this property for n so we'll restrict ourselves to finding just the first pair. How would we write an algorithm to find it?

We can no longer search a finite list of primes for this pair because there is no restriction on the size of the pair, only on their difference. If we were to write a program for this problem it would have to generate primes as it went along. Unfortunately, as long as the proposition remains unproved we can never be sure that our search will succeed. Our program may go on forever!

This question of whether or not a given computer program is guaranteed to stop has major mathematical implications and is discussed further in "What computers can't do" elsewhere in this issue.