Mathematical mysteries: Right angle race

The German mathematician Adam Ries (1492-1559) was the author of the most successful textbook of commercial arithmetic of his day. The book, published in 1552, earned such a high reputation that the German phrase nach Adam Ries is used to this day to indicate a correct calculation.

In An Introduction to the History of Mathematics, Howard Eves tells a story of a friendly contest between Adam Ries and a draughtsman to see who could construct the largest number of right angles in one minute, using only the traditional Euclidean tools of ruler and compasses.

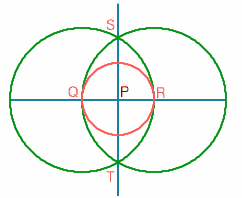
Figure 1: The draughtsman's construct

The draughtsman used a standard school construction, probably the following:

• Draw a straight line AB and mark a point P on it.
• Describe a circle, centre P, cutting AB at points Q and R
• With centres Q and R and radius QR, describe arcs intersecting at S and T.
• Join ST.

Then ST is perpendicular to AB at P, ie the angle SPR is ninety degrees.

The draughtsman repeated this construction at a number of points on AB until his time ran out.

After drawing the line AB, each right angle takes the draughtsman four steps to construct. Assuming each step takes one second, the draughtsman could construct 14 right angles in 57 seconds.

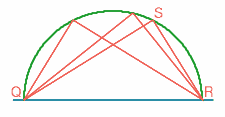
Figure 2: Ries's construct

Adam Ries started by drawing a line AB and then described a semicircle with centre P and diameter QR on it. He then chose a point S on the semicircle and joined QS and RS. Then, since the angle in a semicircle is a right angle, the angle QSR is ninety degrees. Ries repeated this construction at different points on the semicircle until his time ran out.

After drawing the line AB and the semicircle, each right angle requires two construction steps. If each step takes one second, Adam Ries could construct 29 right angles in one minute by this method, winning the contest by a wide margin.

However, if the draughtsman had not performed his constructions all on the same line AB, but had rather erected each successive perpendicular on the previous perpendicular, he could have won the contest easily.

Leaving out the circle arcs and labelling the successive perpendiculars $L_1$, $L_2$, $L_3$, \ldots, the diagram below shows that:

• $L_1$ and $L_2$ each produce one right angle.
• $L_3$ and $L_4$ each produce two right angles.
• $L_5$ and $L_6$ each produce three right angles.
• $L_{2n-1}$ and $L_{2n}$ each produce $n$ right angles.

\par So, after constructing the line $L_{2n}$, a total of $2(1+2+3+\ldots+n) = 2.\frac{1}{2}n(n+1) = n(n+1)$ right angles have been constructed. Since each line after AB takes 4 construction steps, the draughtsman could have constructed $n(n+1)$ right angles in $8n+1$ steps. With $n=7$ (and assuming as before that each step takes one second), the draughtsman could have constructed 56 right angles in 57 seconds, soundly defeating Adam Ries.

You might like to have a go yourself with the applet below. In the toolbox (below right), you will see 5 buttons. These are:

1. A "ruler" - which allows you to draw straight lines between 2 points. Click on it and then click and drag in the main window.
2. A "compass". Click on it and then click and drag in the main window.
3. A moving tool. Not strictly necessary, but useful if your diagram grows too large.
4. An undo tool.
5. A start again tool.

Please enable Java for an interactive construction (with Cinderella).Please enable Java for an interactive construction (with Cinderella).Please enable Java for an interactive construction (with Cinderella).