
Maths in a minute: The brazil nut effect
This article is part of our package on the maths of materials, which is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below.

How's your muesli shaking down?
It is time for breakfast and you reach for your packet of cereal, which is a mix of muesli and nuts. As you pour the cereal into your breakfast bowl you find, much to your surprise, that you get a bowl full of nuts. That's is odd: have the large nuts have risen to the top of the muesli? If yes, then this seems to contradict our intuition that larger objects should go to the bottom.
What you have seen (literally) is an example of the brazil nut effect. It occurs because your cereal packet comes to you having travelled a considerable distance. (To learn more about the movement of food around the world have a look at this article.) During its travels it gets shaken up. It is the shaking which is the key to the brazil nut effect. As the cereal is shaken the nuts may move up a little, leaving gaps beneath them. The smaller and faster moving muesli then flows into these gaps. As it does so, so the nuts rise upwards. Eventually they get to the top of the cereal.
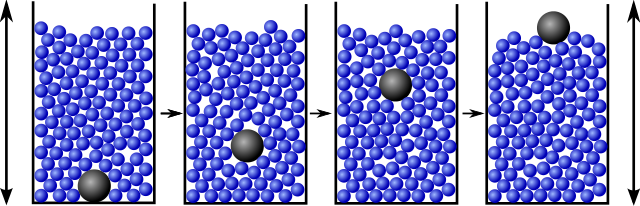
The Brazil nut effect. Image: Gsrdzl, CC BY-SA 3.0.
The brazil nut effect is just one of the counter intuitive properties shared by granular materials, which as the name suggests are materials made up of grains. Granular materials are very important in the food industry. For example, they make up the grain in grain silos, the are the basis of baby food, nuts, rice, coffee, chocolate, custard powder and many cereals such as cornflakes. Granular materials also occur naturally, with snow in large quantities being a good example, and sand another (find out more here). Many of the fascinating patterns seen in sand dunes are a consequence of sand being a granular material.
Another context in which granular materials play a role is in the manufacture and storage of paint powders, fertiliser, cement and even sand. Mathematics is used to predict how granular materials can flow. In some sense, granular materials do not constitute a single phase of matter, but have characteristics similar to solids, liquids or gases, depending on the average energy per grain. However, in each of these states granular materials also exhibit properties which are unique to them. Indeed, granular materials also exhibit a wide range of pattern forming behaviours when excited (e.g. vibrated as above, or allowed to flow).
Different behaviours arise depending on whether the grains can move freely over each other, or if they can get jammed. The latter is certainly what you don't want in a grain silo. Mathematics plays a critical role in predicting whether jamming will or will not occur, and by doing this helps to feed the world.
About this article
This article is based on a talk in Budd's ongoing Gresham College lecture series. A video of the talk is below.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.