If we humans wanted to scale vertical walls like Spider-Man, 40% of our body would have to be covered in sticky footpads. This would require very large sticky feet with shoes in European size 145 or US size 114.
A gecko and its sticky feet.
These numbers have recently been estimated by a team of zoologists at the University of Cambridge. Their new study, published in PNAS, explains why nature hasn't produced adhesion-based climbers larger than the gecko. As the size of a climbing animal increases, the percentage of body surface that needs to be covered by sticky pads increases too, setting a limit to the size of animal using this strategy: larger animals would require very big feet. The necessary shape changes would make the evolution of this trait impractical.
David Labonte and his colleagues based their study on a simple geometrical observation. "As animals increase in size, the amount of body surface area per volume decreases – an ant has a lot of surface area and very little volume, and an elephant is mostly volume with not much surface area," explains Labonte.
You can get an idea of why this is true by imagining for a moment that all animals are spherical. The surface area of the sphere of radius 
is
![\[ 4\pi r^2. \]](/MI/1fd6301227928d782348306d7bb1fa5a/images/img-0002.png) |
The volume of the sphere is
![\[ \frac{4}{3}\pi r^3. \]](/MI/1fd6301227928d782348306d7bb1fa5a/images/img-0003.png) |
Surface area per volume is therefore
![\[ \frac{4\pi r^2}{\frac{4}{3}\pi r^3} = \frac{3}{r}, \]](/MI/1fd6301227928d782348306d7bb1fa5a/images/img-0004.png) |
which decreases as the size of the sphere, measured by , inreases: the larger the sphere, the smaller the amount of surface area per volume. And while animals aren’t usually spherical, their shapes aren’t outlandish enough to defy the inverse relationship between surface area per volume and size. This means that, to hold its weight, a larger sticky climbing animal needs to cover a larger proportion of its body in sticky pads than a smaller one.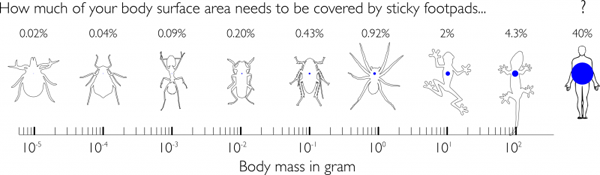
How sticky footpad area changes with size. Image: David Labonte.
The researchers compared the weight and footpad size of 225 climbing animal species including insects, frogs, spiders, lizards and even a mammal. "We covered a range of more than seven orders of magnitude in body weight, which is roughly the same weight difference as between a cockroach and Big Ben," says Labonte. "Although we were looking at vastly different animals – a spider and a gecko are about as different as a human is to an ant – their sticky feet are remarkably similar," says Labonte.
"Adhesive pads of climbing animals are a prime example of convergent evolution – where multiple species have independently, through very different evolutionary histories, arrived at the same solution to a problem. When this happens, it's a clear sign that it must be a very good solution."
Not bigger, but stickier
There is, however, one other possible solution to the problem of how to stick when you're a large animal, and that's to make your sticky footpads even stickier. "We noticed that within some groups of closely related species pad size was not increasing fast enough to match body size yet these animals could still stick to walls," says Christofer Clemente, a co-author from the University of the Sunshine Coast. "We found that tree frogs have switched to this second option of making pads stickier rather than bigger. It's remarkable that we see two different evolutionary solutions to the problem of getting big and sticking to walls."
"Across all species the problem is solved by evolving relatively bigger pads, but this does not seem possible within closely related species, probably since the required [shape] changes would be too large. Instead within these closely related groups, the pads get stickier in larger animals, but the underlying mechanisms are still unclear. This is a great example of evolutionary constraint and innovation."
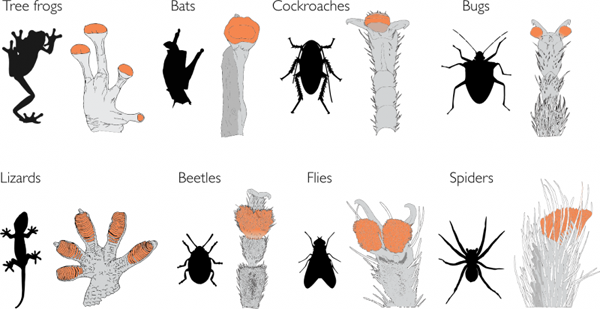
Different types of sticky feet. Image: David Lahonte.
The researchers say that these insights into the size limits of sticky footpads could have profound implications for developing large-scale bio-inspired adhesives, which are currently only effective on very small areas. "Our study emphasises the importance of scaling for animal adhesion, and scaling is also essential for improving the performance of adhesives over much larger areas. There is a lot of interesting work still to be done looking into the strategies that animals use to make their footpads stickier - these would likely have very useful applications in the development of large-scale, powerful yet controllable adhesives," says Labonte.
This article is adapted from a press release by the University of Cambridge, reproduced under CC BY 4.0.
