Maths in a minute: Trisecting the angle

Can you divide an arbitrary angle into three equal parts using only a ruler and straightedge?

One of the most famous problems in the history of mathematics is how to divide an angle drawn on a piece of paper into three equal parts using just a compass and a straightedge (that's a ruler without markings). Of course, you can easily measure any given angle using a protractor, divide the number you get by 3, and then measure off the desired third of the angle using the protractor again. But the point is that the protractor is prohibited — you're only allowed a compass and a straightedge. The problem goes back to the ancient Greeks, who did a lot of their geometry using only these two tools.

To get a flavour of how this sort of problem might be solved, let's start by dividing a given angle into two equal parts, rather than three.

Bisecting an angle

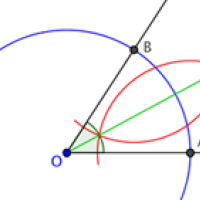
Given two lines that meet at a point you can bisect the angle between them as follows. Put the point of the compass at and draw a circle (of any radius you like). This is the blue circle in the diagram. The circle will cross the two lines at two points: call these a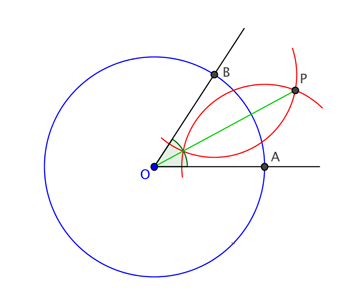nd .

Bisecting an angle.

Now put the point of the compass at and draw an arc of a circle, as shown in the diagram.

Without changing the radius at which the compass is set, move its point to and draw another arc of a circle. These are the red arcs in the diagram. The point where the two red arcs cross, can then be joined to using the straightedge (the green line). The angle is exactly half of the angle . (If the red arcs don’t cross, then you need to use larger circles!)

It's possible to prove that this method bisects any angle. You can try this for yourself (use similar triangles) or see a proof here.

Trisecting an angle

What about dividing an angle into three equal parts? Why is that so difficult? There are a few special cases of angles for which it can be done — for example if the angle is equal to radians or 90 degrees (see this video). You can trisect any angle if you allow yourself to use an extra dimension (see here). It's also possible to trisect an arbitrary angle if you use a ruler, rather than a plain straightedge, so that you can measure distances. However, to play by the rules you aren't allowed any marks on the straightedge at all — it must be completely blank.

The problem of whether a general angle can be trisected remained a mathematical mystery for millennia — it wasn't until 1837 that it was proven impossible by Pierre Wantzel, a French mathematician and expert on arithmetic. This was a great achievement for a man of 23, who subsequently died at the tragically young age of 33.

So why is it impossible? Wantzel showed that the problem of trisecting an angle is equivalent to solving a cubic equation using a straightedge-and-ruler construction. He also showed that only very few cubic equations can be solved in this way — most cannot. He thus deduced that most angles cannot be trisected.

Never give up

Since Wantzel's proof we know for sure that an arbitrary angle can't be trisected using a ruler and compass, but this doesn't stop people trying. Here at Plus we regularly receive emails from people who think they've cracked the problem. Needless to say, all these so-called proofs contain flaws. But there are some ways to trisect and angle, if you change the rules a little. You can find out more in Trisecting an angle with origami and Trisecting the angle with a straightedge.