
Trisecting an angle with origami
Over 2000 years ago the Greek mathematician Euclid of Alexandria laid down the foundations of geometry. But Euclid's geometry was very different from ours. It was all about the geometric shapes you could produce using just a straightedge (a ruler without markings) and a compass. You can do lots of useful things with these tools. For example, you can such divide an angle into two equal halves:.
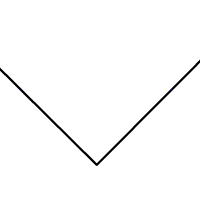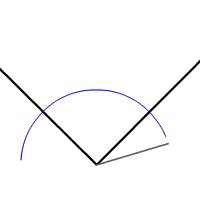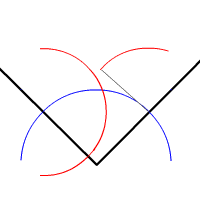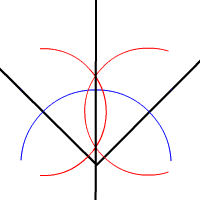
If you can divide an angle in two, which is called bisecting an angle, you might think you could also trisect an angle, that is, divide it into three equal parts. But try as he might, Euclid and every other mathematician in the centuries since could not manage it.

Euclid of Alexandria
The problem of whether angle trisection could be done in the general case remained a mathematical mystery for millennia. Many mathematicians, both amateur and professional, have tried. It was finally shown, in 1837, that it was impossible by Pierre Wantzel, a French mathematician and expert on arithmetic. This was a great achievement for a man of 23, who subsequently died at the tragically young age of 33.
So why is it impossible? Wantzel showed that the problem of trisecting an angle is equivalent to solving a cubic equation (you can read why this is true here). Moreover, he showed that only very few cubic equations can be solved using the straightedge-and-compass method — most cannot. And so he realised that most angles cannot be trisected.
This hasn't stopped people trying — here at Plus we still occasionally get letters from people saying they've finally found the way to trisect an angle using Euclid's tools.
But we can trisect an angle if we use a different tool: origami. It turns out that paper folding is more powerful than straight edge and compass. Here is how you trisect and angle with origami. Each step consists of a single fold and represents one of the basic single-fold moves you can make. These basic folds are called the axioms of origami, with reference to the axioms of Euclid's geometry, which describe the basic facts underlying it (you can find out more about the axioms of origami here).
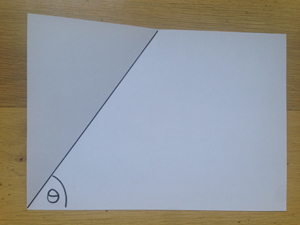
First of all mark out your angle. You can do this with a single fold running through the bottom corner of the paper.

Here is the angle θ we'd like to trisect:
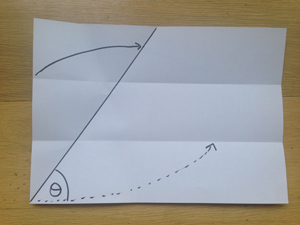
The first step is to make a fold that is parallel to the bottom edge of the paper, as the bottom edge represents one of the boundaries of our angle. You want this fold to be somewhere in the top half of the piece of paper. So pick a point in the top half and make a fold through that point so that the fold is perpendicular to the side of the sheet (by neatly folding the side of the sheet onto itself). This way, your fold is parallel to the top and bottom of the paper.

Now fold up the bottom of the paper to meet your horizontal fold in the top half of the sheet.

You should now have two horizontal folds, parallel to the bottom of the paper.

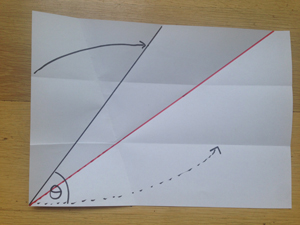
The next step is a little trickier. You want to make a fold that matches two points to two lines. You want the point where your upper horizontal fold meets the edge of the paper to end up on the angled line marking the boundary of your angle. And you want the bottom left corner of the paper to end up on your lower horizontal fold. It takes a bit of fiddling to get the placing of the fold right before you make the final crease, but persevere because you can do it!
Phew! Here is what it should look like:

You'll notice that now the lower horizontal fold runs at an angle up the page on the part that has been folded over, indicated in red in the picture. Fold along this angled line.

Now if you open the sheet out you'll see that this has produced a fold that runs toward the bottom left corner, within the boundaries of our original angle.

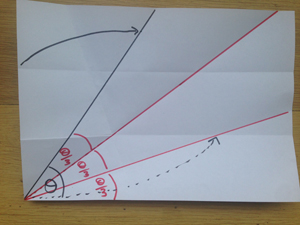
Now that the paper is opened out, make that fold again so it runs all the way to the corner.

You should now have this:
The final step is to fold the bottom edge of the paper up to meet this new fold.

Open it up and hey presto... you've trisected the angle! You've solved an ancient problem with a few folds!
See here for a proof that this really works and here for more on the power of origami.
About the author
Rachel Thomas is Editor of Plus.
About this article
This article was inspired by content on our sister site Wild Maths, which encourages students to explore maths beyond the classroom and designed to nurture mathematical creativity. The site is aimed at 7 to 16 year-olds, but open to all. It provides games, investigations, stories and spaces to explore, where discoveries are to be made. Some have starting points, some a big question and others offer you a free space to investigate.
Comments
Anonymous
Come on, what the folding operations really do is quadrisect the bottom left right angled corner of the sheet into four 22.5 degree angles. That first fold, followed by an unfold again, is a means of getting away with designating the remaining three of those angles by the single cover name "theta" in advance, so he/she can later claim "Look everybody, I trisected theta".
Anonymous
Following the post above, I can now see that it was me that was inadvertently quadrisecting the bottom left corner. I also failed to recognise that with the very first fold defining the angle to be trisected, you can create a pair of angles in any size ratio you want, not just 1:3 due to some strange property of folded paper, which is what I was vaguely thinking. I did it again with a better understanding, with the correctly interpreted results this time. My apologies.
Anonymous
I'm not convinced. The step 4 is very problematic and the very calling of a trial and error attempt shows that. If we give the compass and the straightedge the same possibility (trial and error), wouldn't we be also able of trisecting an angle?
Marianne
The "trial and error" only referred to the fact that you need a little folding skill to get this step right, so you might need to fiddle a little. The important point is that there always exists a unique fold that does the trick.
Tej
That's the thing... You can do this using a marked straight edge and a compass ... Not an unmarked one