The buzz on bumblebees
The common bumblebee is a familiar visitor to European gardens. At first sight there's nothing particularly remarkable about this small furry interloper, but it has been a source of mathematical controversy for nearly a century.
Calculations made in the 1930s at the University of Gottingen seemed to prove that it was aerodynamically impossible for a bumblebee to fly. Bumblebees, of course, continued to fly about with blithe disregard for these results!
The so-called "Bumblebee Paradox" entered the public imagination, even inspiring the title of a well-known children's book ("The Bumblebee Flies Anyway", by Robert Cormier).
Confusion persisted right up until 1996, when researchers at the University of Cambridge's Department of Zoology built scaled-up robotic models of insects to study in detail the airflow around their flapping wings.
This team, headed by Animal Mechanics specialist Charlie Ellington, found results that seemed to solve the conundrum. They discovered that extra aerodynamic lift was generated by a vortex travelling along the leading edge of the insect's wings during a downstroke.
However, it seems that the Bumblebee Paradox may not be so easily defeated. Researchers Michael Dickinson and James Birch, from the University of California at Berkeley, have recently suggested in the journal Nature that the bumblebee may be as baffling as ever.
To avoid the difficulty of building and working with tiny mechanical insects, they built a greatly scaled-up model of a fruit fly and observed it flapping in a tank of mineral oil. This simulated the experience of a tiny real-life fruit fly flapping in the much thinner medium of air.
"Based on these experiments we concluded that the [Cambridge] hypothesis cannot explain the attachment of the vortex throughout the stroke," said Professor Dickinson. So how does the bumblebee fly? "We still don't know for sure" - and the bumblebee flies anyway.
Behind the news: The Reynolds Number
In using a scaled-up model of an insect, flapping in oil rather than air, the Berkeley team were taking advantage of an important property of fluid-dynamical systems known as the Reynolds Number.
Consider a simple system where a fluid is flowing around a small pebble, as shown in figures 1 and 2 below. (This system has the same properties as a system with a small object moving through a still fluid.)
The behaviour of the fluid as it flows around the object can be usefully characterised by a single number, the Reynolds number. In this case, the Reynolds number is defined by the length of the object, $L$, the velocity of the flow, $U$, and the {\em viscosity} of the fluid, $\nu$. (Viscosity measures the resistance of the fluid to flowing; treacle, for example, is more viscous than maple syrup, which is more viscous than milk). \par The Reynolds number $R$ for our simple system is defined by: \begin{displaymath} R = \frac{UL}{\nu} \end{displaymath}
Figure 1 shows the fluid flow we can expect when the Reynolds number is low: this smooth progress of the fluid around the object is known as laminar flow.
Figure 2 shows the fluid flow we can expect when the Reynolds number is high: the swirling effect behind the object is known as turbulence, which featured in a very early Plus article.
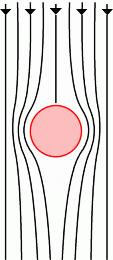
Figure 1: |
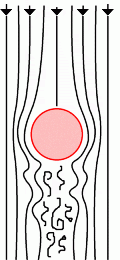
Figure 2: |
The fact that the Reynolds number determines the nature of the flow means that we can make quite different systems behave similarly by ensuring that the have the same Reynolds number.
In other words, if we increase the length of the object $L$, we can balance this by increasing the viscosity of the fluid $\nu$ by the same factor. Hence, a large model bee flapping in more viscous oil can be a useful experimental model for a small actual bee flapping in less viscous air.