
Lambda marks the spot — the biggest problem in theoretical physics
The mathematical maps of theoretical physics — the Standard Model of particle physics and the Big Bang model of cosmology — have been highly successful in guiding our understanding of the Universe at the largest and smallest scales. Linking these two scales together is one of the golden goals of theoretical physics. But at the point where these maps merge, at the very edges of our understanding of these fields, lies one of the most controversial concepts in physics: the cosmological constant.
A very tiny map
When repairs at the Large Hadron Collider are finished this summer, the hunt for the Higgs boson will resume. But how do the LHC physicists know what they are looking for? How do they come up with theories that predict particles they have never seen? Just how does theoretical physics work anyway?
Occasionally, advances in theoretical physics are due to intuition alone. But most of the time physicists have a map to guide them, a mathematical map of the Universe, which tells them what to expect to find and how things should behave.

One such map is the Standard Model of particle physics. While most of us still have a picture in our heads of atoms having a hard centre of protons and neutrons, with electrons whizzing about them, the current understanding of the smallest building blocks of matter is more sophisticated. The Standard Model describes the interactions of 12 fundamental particles and the force carrying particles for the fundamental forces of electromagnetism and the strong and weak nuclear forces. (You can read more about the Standard Model in The physics of elementary particles and this issue's Particle hunting at the LHC.)
The mathematics is based on the underlying symmetries that govern these fundamental forces. For example, the electromagnetic field around a conducting wire is symmetrical around the wire — you can rotate the wire (around an axis running along the wire) and it won't affect the electromagnetic field. This kind of symmetry is described by the group of rotations on a circle, called U(1), and this defines how particles behave in an electromagnetic field. (You can read more about symmetry and group theory on Plus in The power of groups and Through the looking-glass.)
The symmetry groups provide the framework for all the possible ways these fundamental particles and forces can interact, enabling physicists to write down equations, called Lagrangians, predicting these possible interactions. As you would expect, these equations are incredibly complicated and can involve an infinite number of terms. But with a deft mathematical manoeuvre, called renormalisation, these unwieldy equations can be turned into something very useful when operating within certain limits: an effective theory that allows definite predictions about physics at the quantum scale.
These effective theories have been incredibly successful, mapping out the landscape of particle physics for much of the last century. In fact, almost everything predicted by the Standard Model has now been experimentally verified. For example, Wolfgang Pauli predicted the existence of neutrinos in 1930, in order to preserve the conservation of energy and momentum in a type of radioactive decay. Physicists in the 1960s then realised that there were more than one type of neutrino, and in 2000 the final type, the tau neutrino, was observed in an experiment at Fermilab in the US. The final piece of the puzzle of the Standard Model is the Higgs boson, which will hopefully be observed at the LHC when it starts up again later this year. (You can read more in Particle hunting at the LHC.)
Boldly going where no one has gone before
The Standard Model has proved stunningly effective up to the energies accessible so far — about 1 TeV or 1012 electron Volts, which is about a tenth of the energy particles will have in the LHC. An important question is whether new physics will be seen at the LHC, or whether the Standard Model will continue to hold sway all the way up to the Planck scale of 1015 TeV (where quantum gravity must necessarily come into play). An important clue to where the cut-off of the Standard Model might be (such that the model no longer applies for energies above this cut-off) comes from observing the behaviour of two terms in the Lagrangian which increase with the cut-off energy.
One of these terms is the radiative correction to the Higgs mass, which describes how the Higgs boson is affected by its interactions with other particles. "As the Higgs boson is a fundamental scalar it sees all particles propagating in the vacuum, and it couples to their mass, and therefore it gets a correction to its own mass," says Subir Sarkar, professor of theoretical physics at the University of Oxford. This correction is proportional to the square of the cut-off energy, so if the Standard Model does work all the way up to the Planck scale then the Higgs boson's mass is predicted to be far larger than the value that could exist in nature, according to experimental results.
The solution that physicists have come up with is to invoke a new symmetry of nature — a supersymmetry between the fundamental particles associated with matter and forces — which would cancel this mass correction altogether. However, supersymmetry cannot be exact since it would then predict that all the particles in the Standard Model have superpartners of exactly the same mass — and this is not the case. "Thus supersymmetry must effectively be broken such that the superpartners are no lighter than about a TeV - that would explain why they haven't been observed yet ... but they should then be seen in the forthcoming high energy collisions at the LHC," says Sarkar.
So the effective cut-off of the Standard Model may be no higher than about 1 TeV — and at higher energies exciting new physics like supersymmetry would come into play. We now have to consider the second term which also increases with the cut-off energy. Quantum physics predicts that, far from being empty, the vacuum consists of a seething mass of virtual particles that pop in and out of existence, and these fluctuations contain energy. This vacuum energy is proportional to the cut-off energy raised to the power of 4, so would be at least 1048 electron Volts. "However this has no influence on any measurement we can make in the laboratory so particle physicists can forget all about vacuum energy," says Sarkar.
The view from the quantum world
But can we? It turns out that the predictions of vacuum energy seem to be where particle physics and cosmology weave together. Good news, perhaps, in the grand schemes of unifying the two scales of physics into a Theory of Everything. However, it turns out that this reach of the particle physics map suggests a very different landscape to the one observed at cosmological scales.
According to Sarkar, the Standard Model has provided a fantastic guide to the quantum world, but we are now reaching a point where this map is no longer useful. "This is a game with precise rules, and it has delivered more than the originators ever expected. And the present status of this game is to use this effective field theory philosophy to understand how to parametrise new physics that we are interested in, particularly because of the relevance for cosmology. The real problem is in the cosmos: now you have general relativity ... and gravity. "
General relativity and the Hot Big Bang
The Standard Model of particle physics has done an excellent job of describing the effects at the quantum scale of the electromagnetic, strong nuclear and weak forces. However, one fundamental force is missing: gravity. And despite initial optimism about string theory, no one has been able to extract from it a detailed theory of how gravity behaves in the quantum world.
Newton's gravitational force
Force = -GMm/r2
where G is Newton's gravitational constant, M and m are the masses of the two objects, and r is the distance between their centres.
However, gravity is well described at classical and cosmological scales. Newton's theory of gravity, the familiar inverse square law, works well on the scale on which we live our lives. In 1915 Einstein generalised Newton's laws to the largest scales, by explaining that gravity was caused by masses warping spacetime. He applied his theory of general relativity to our Universe, and so modern cosmology began.
Einstein's theory is described by a set of complex equations, called Einstein's field equations. These are incredibly difficult to solve exactly, which is necessary to make concrete predictions about the evolution of our Universe. Exact solutions describe the shape of spacetime for certain assumptions. The first nontrivial solution, the Schwarzschild metric, provided a description of the Sun's gravitational field and the motions of the planets, and later led to the first description of a black hole.
The Hot Big Bang model of cosmology, the model currently used to understand our Universe, is based on a solution of Einstein's field equations based on an important assumption — that spacetime is isotropic and homogeneous. This means that on a large scale no particular point in space is special: it doesn't matter where you start out in the Universe, or which direction you look, space-time will look pretty much the same.
Developed over the 1920s and 30s by four mathematicians, the Friedmann-Lemaître-Robertson-Walker metric describes the geometry of the Universe and how it changes with time. Because this model assumes the Universe is pretty much the same everywhere and in every direction, the three dimensions of space, x, y and z, can be described by one radial coordinate, a, that is a measure of the scale of the Universe. The model essentially is a description of how this scale factor changes with time.
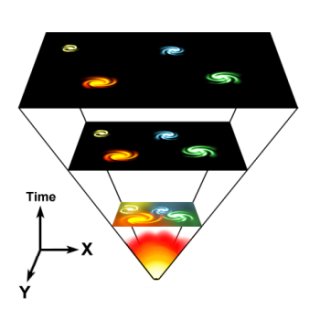
According to the Big Bang model, the universe developed from an extremely dense and hot state. Space itself has been expanding ever since, carrying galaxies (and all other matter) with it.
This model, which predicts that the Universe expanded from a hot dense state and continues to expand today, has proved very successful. Theoretical predictions have driven observational programmes and many have been confirmed. The predicted bending of light by gravity has since been observed and is now used as a technique to explore the Universe's hidden treasures, such as black holes. Predictions about the relative amounts of light elements such as helium and deuterium created in the early moments of the Universe, and the nature of the cosmic background radiation, have also matched observational data. You can read more in The four pillars of the Standard Cosmology.
Einstein's big mistake?
As with all efforts to explore the unknown, the path to the standard model of cosmology has not been straightforward. In 1915 when Einstein first used his theory of general relativity to describe the Universe, what he found did not fit with his world picture. The gravitational force of matter would cause the Universe to collapse back in on itself. But Einstein believed the Universe was static — it neither expanded nor contracted. In order to balance the gravitational attraction of matter, he included a repulsive term and set the constant in this term, called the cosmological constant, to have a particular value. This value forced his field equations to describe a static Universe.John Barrow, Professor of mathematical sciences at the University of Cambridge, explains that this gives the force of gravity an additional part: a repulsive force associated with the cosmological constant. "If you think of Newton's famous inverse square law of gravity, because it's attractive we would say the force has a minus sign, so it's equal to -1/r2 where r is the distance between objects. Now if you add to that another positive force that is proportional to distance, a λr term, gravitational force becomes:"
"And when distances are small the -1/r2 term is the biggest and governs what we see on Earth, and in the solar system, and in our galaxy. But as you look to bigger and bigger distances, the -1/r2 term is getting smaller and smaller. However, the λr term is getting bigger and bigger, and eventually it takes over in the Universe on a big enough scale. And when it does, the effective force of gravity changes to being repulsive."
Einstein believed that the Universe was static and had a constant radius R. And in order to force his equations to describe this static Universe, he chose a value for λ such that the total gravitational force in the Universe would be zero. That is:
(In fact Einstein wasn't the first to realise that the laws governing gravity may have this extra repulsive term; you can read more about the history of λ from Newton to Einstein in Barrow's regular Outer space column.)

An image taken by the Hubble Space Telescope showing stars in the Globular Star cluster NGC 6397, about 8500 light years from the Earth. Edwin Hubble discovered that the Universe was expanding, and stars such as these were rushing away from us. Image courtesy NASA.
To Einstein's dismay, it was quickly shown that a static Universe was not stable and the slightest nudge would set it expanding or contracting. Then shortly afterwards, in 1928, Hubble discovered evidence that the Universe was expanding (read more in this issue's Hubble's top five scientific achievements). Einstein reportedly called the cosmological constant his "biggest blunder" and retracted it.
However, Sarkar says the inclusion of the repulsive term wasn't the problem: "It certainly was not a blunder to point out that there was this term in his equation. That was a mathematically correct statement; the term is allowed because of the underlying symmetry. [However] choosing it to have a specific value was his choice and indeed that was not right." Though perhaps Einstein can be forgiven this misjudgement: given the continued relevance of his work today, we sometimes forget how different the Universe looked in the early twentieth century. "At the time we only knew our own galaxy, we didn't even know other galaxies [existed], far less that they were rushing away from us," says Sarkar.
But the cosmological constant wasn't completely forgotten, often retained in the equations of cosmology but usually assumed to be zero. "Everyone has known since 1915 that this term is possible — you can choose to set it equal to zero or you can include it," says Barrow. "The reason people always retained Einstein's idea, and didn't just throw it away, was because it was recognised that having this constant in the theory of gravity was a way for particle physics and quantum theory to be linked to gravity. In modern physics this constant is interpreted as the vacuum energy of the Universe."
The problem with Lambda
And here is where the maps of the quantum and cosmological scales start to merge. As we saw before, the Standard Model predicts that quantum fluctuations in empty space would contribute to a vacuum energy, but the huge values predicted had seemed dubious and most physicists believed that supersymmetry exactly cancelled these out. This seemed like the right sort of approach, as it agreed with the belief of most cosmologists that the cosmological constant was zero.
However, the picture changed dramatically in 1998 when data from supernovae, and from other experiments since then, suggested that the Universe is not only expanding, it is expanding at an accelerating rate.
The possibility that the Universe was accelerating revived interest in the cosmological constant, and the term dark energy was coined to describe the mysterious vacuum energy of empty space. "We can understand and describe what is happening very accurately using this old idea of Einstein that there is this other constant of nature, this cosmological constant, which gives this λr force. So the equations all work perfectly and we can describe it very, very well," says Barrow.

Observations made by the Hubble Space Telescope, such as these, have narrowed down the possible value of the cosmological constant. Image courtesy NASA.
So vacuum energy now seems to play a part at the largest and smallest scales of physics: and here lies the problem. It appears that the cosmological constant is not zero, and the acceleration of the Universe is being driven by vacuum energy. However, the view from cosmology looks different from the quantum world. The vacuum energy predicted by the Standard Model of particle physics is around 1060 times bigger than the vacuum energy calculated from the observed acceleration of the Universe. The numbers aren't just a bit out, they are wildly incompatible. And if the cosmological constant did have the value predicted by the Standard Model, the Universe would have been driven into acceleration just an instant after the Big Bang, and no galaxies, stars or planets would have ever formed.
The cosmological constant represents the biggest problem in physics today. "If new observations came in tomorrow and showed we were wrong, and the cosmological constant was zero, 99% of physicists would breathe a sigh of relief," says Ben Allanach from the University of Cambridge. If it was exactly zero, the massive prediction for vacuum energy from quantum physics could be cancelled out in the equations using symmetry. But symmetry can only cancel things out exactly: if vacuum energy and the cosmological constant are just a little bit above zero, as observations seem to suggest, this argument no longer works. And so far no one has come up with an explanation of how to reconcile the numbers.
A mirage, or the beginning of a new map for physics?
Sarkar says that particle physicists were always aware that the massive prediction for vacuum energy was a problem, but as it was a problem only at the very limits of the Standard Model, it didn't affect particle physics experiments in the laboratory. "But now it has come back to haunt them at the only context it can be relevant — the cosmological one."
"So far nothing has addressed this skeleton in the closet, including string theory," says Sakar. "But rather than see this as failure, [we should] see it as wonderful opportunity. It means there is something really fundamental for us to discover, something really exciting for us to find out, which is the solution to the cosmological constant problem." And most physicists agree that this solution will involve a new theory of quantum gravity.
However, there is another worry about the cosmological constant, called the coincidence problem. The value calculated from observations means that it would only drive the Universe into acceleration relatively recently (cosmologically speaking), which just happens to coincide with when we are around to observe its effects. "Not only does the cosmological constant need to be cancelled nearly to zero," says Sarkar, "it also has to have a tiny value on top of zero that is just relevant today." Is this too much of a coincidence?
Some physicists, including John Barrow, believe that the particular value of the cosmological constant may come down to chance. He says that just like the final resting place of a ping pong ball dropped onto a corrugated iron roof, the value of the cosmological constant might be determined at random. "And all we can say is that we couldn't be talking about a situation where it was much bigger, because there wouldn't be any galaxies or stars. But more than that we can't really say."
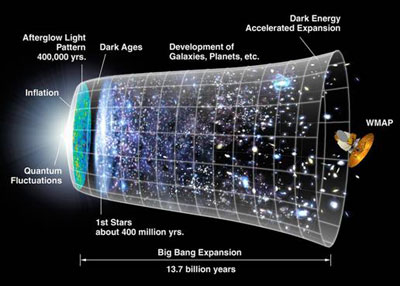
The current map of the Universe. Image courtesy NASA.
But Sarkar and others believe the coincidence problem might be down to the fact that we are using the wrong mathematical map. "Nobody has seen [dark energy], or seen any acceleration. They have seen a nonzero value for an unconstrained term in the simple model they use to interpret the data, which would then imply a vacuum energy density that would have the necessary properties. And the model appears to fit data very well."
Sarkar says that the attempts to explain dark energy have stimulated lots of interesting activity thinking about gravity and extra dimensions. "A lot of good has come out of this, but the bottom line is that it may well be a cosmic mirage, it might just be an artifact of this model that we use to interpret the data."
Perhaps the Universe is more complicated than we originally thought, and the assumptions that it was roughly the same everywhere, and looked the same in all directions, is not correct. Some physicists are exploring the possibility that we need to redraw the cosmological map. Perhaps we are sitting in some large irregularity in the Universe, a big hole, and as we look out this change in the density in the Universe between our region and its surroundings can mimic the effect of acceleration. Sarkar hopes that as the sensitivity of our experiments and observations increase, we will see that the isotropic and homogeneous model of the Universe is an oversimplification.
So just what is the answer? How does gravity work at the quantum level? And is the tiny value we observe for the cosmological constant a cosmic mirage; do we need to redraw our map of the Universe? We'll just have to wait and see what the explorers at the boundaries of theoretical physics discover. Sometimes you just have to look up from the map and step into the unknown, and see what you find.
About this article
Rachel Thomas is co-editor of Plus.

Subir Sarkar

Ben Allanach

John D. Barrow
For this article Rachel interviewed Professor Subir Sarkar, University of Oxford, Professor John Barrow and Dr Ben Allanach, University of Cambridge. Rachel would like to thank Professor Sarkar, Professor Barrow and Dr Allanach for their enthusiasm and un-ending patience in trying to explain the mysteries of the Universe to a novice.
Comments
Anonymous
Why do we assume inflation is up and out, we pay too much attention to our senses,there are other directions. The schwarzschild radius is constant but it doesn't prevent space from being skewed within it, can you make an observation that proves we are not falling into space rather than being exploded into it? Dark energy is the difference in the geometry of space caused by the very large mass way over there ---->. That which gravity is moving us towards.