Runners and cyclists can tolerate heat and cold but the thing they dislike most is wind. They know it produces slower lap times on loop courses. Can we show them why?

where $\rho$ is the density of air. The magnitude $F$ of the drag force you will feel is $$F=\frac{1}{2}\times \rho \times A\times V^2.$$ The rate of energy use, or power $P$, needed to overcome the air's resistance is equal to $F\times V$, so $$P=\frac{1}{2}\times \rho \times A\times V^3.$$ In practice, the quantity $A$ depends on the aerodynamic quality of what you are wearing and your degree of streamlining as well as your geometrical area. We split it up as two parts $A=A^{\prime }\times c$, where $A^{\prime }$ is the geometrical cross-section and $c$ is a drag factor, which takes shape and clothing texture into account, and typically is $c\simeq 1$. So the power needed to run at speed $V$ through still air is $$\frac{1}{2}\times c\times \rho \times A^{\prime }\times V^3.$$ A top class sprinter with a mass of $70kg$, moving through air of density $1.2kg/m^3$, with body area $A=1.8\times 0.3m^2$ and drag factor $c=1$ will use about 3\% of their energy overcoming still air resistance. 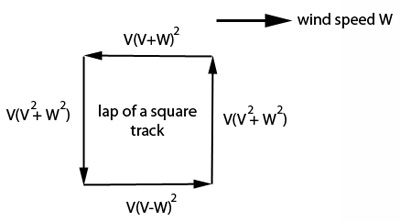What if there is a wind blowing? If the wind speed is $W$ the drag force to be overcome will be proportional to $(V-W{)}^2$ if $W$ is a tailwind and $(V+W{)}^2$ if it is a headwind. Notice there is an asymmetry in this formula because the dependence on the speed is a square. If you ran at $4m/s$ with a following wind of $W=2m/s$ then $(V-W{)}^2=4m^2/s^2$ where if there is a headwind of $W=2m/s$ then $(V+W{)}^2=36m^2/s^2.$ If there is a crosswind then you feel the vector resultant of the oncoming wind that you are running through at speed $V$ and the perpendicular crosswind $W$. The magnitude of the resultant velocity is therefore $(V^2+W^2{)}^{1/2}$ (at an angle $\theta$ to your direction of motion, where $\tan \theta =W/V$.) The magnitude of the drag force experienced is proportional to its square $V^2+W^2.$ The power needed to run at speed $V$ through a crosswind is therefore proportional to the product of the running speed and the drag force, that is $V(V^2+W^2).$ We will assume that the area you present to the wind coming in at angle $\theta$ is the same as it is in your direction of motion, although it might well be slightly bigger. The asymmetry noted above enables us to understand why it is always harder running laps in the wind than in windless conditions: you never gain from the tailwind what you lose into the headwind. For simplicity, suppose you run around the four sides of a square track at speed $V$ and the wind is blowing horizontally from left to right at speed $W.$ The power expended on the first (right-hand vertical) and third (left-hand vertical) straights is just proportional to $V(V^2+W^2)$ but on straight two (into the headwind) it is proportional to $V(V+W{)}^2$ while on the fourth straight it is proportional to $V(V-W{)}^2$ because the wind is following. If we add these four together we get $$\text{Total power per lap }\propto V(2V^2+2W^2+V^2+W^2+2VW+V^2+W^2-2VW)=4V(V^2+W^2)$$% You see that the smallest running power of $4V^3$ is required when there is no wind ($W=0$): the power is always bigger with any non-zero wind speed. The best racing strategy for runners in races that cover many laps is also clear. When you are running into the wind you should try to shelter behind other runners to avoid feeling the full force of the wind. Most runners appreciate this slip-streaming trick but they often don't recognise the other part of the optimal strategy. When the wind is behind you, move out to make sure there is no one directly behind you shielding you from feeling the full benefit of the tailwind. This won't make running in the wind easier for you than when the air is still but it will make it easier than it is for your rivals.