
Outer space: Cushioning the blow

Most of us are familiar with the existence of a sweet spot on a tennis racket or a bat, where it is best to strike the ball. What "best" means is that there is no reaction on your hand at the place where you are holding the bat. This spot is located where the movement of the bat as a whole in response to the force from the incoming ball is equal and oppositely directed to that created by the rotation of the bat about its centre of gravity. Physicists call this sweet spot the centre of percussion and it occurs at a distance from the handhold of a cricket or baseball bat that is about two-thirds of its total length.
Snooker and pool balls have sweet spots too. If you strike a ball with the cue parallel to the table, then where you strike it determines how it will move. The point of contact with the table acts like the pivotal point where you grip the bat. Obviously if you aim your cue shot through the centre of the ball, then the ball will slide as a whole across the table without any rolling. Strike it a little higher than the centre, and it will both slide and rotate. The sweet spot for the ball is the point on the ball where the speed away from the cue caused by the sliding is equal to the rotational velocity in the opposite direction caused by its rolling. Hit the ball at the height of this sweet spot, and it will not slide. It will start rolling straight away.
Where is this special spot?
The height of the sweet spot above the table is $$h=r+I/Mr,$$ where $r$, $M$, and $I = \frac{2}{5}Mr^2$ are the radius, mass and moment of inertia of the ball, respectively. So, we see that $h = \frac{7}{10} \times 2r$; that is, the sweet spot is at a height equal to 0.7 times the diameter ($2r$) of the ball.
I thought that this would tell me the height of the cushion around the sides of a pool or snooker table. My reasoning was that you should design a table for a cue ball game so that the rebounds of the balls from the sides of the table are as smooth and true as possible. If the height of the point of impact was 0.7 times the ball diameter, it would mean that after a ball hit the cushion it wouldn't slide across the table, just roll, losing very little energy in the process.
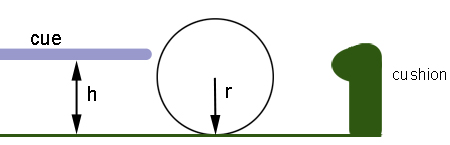
The ball's sweet spot is at a height h above the table, where h is equal to 0.7 times the ball's diameter. The cushion height is only 0.63 times the height's diameter.
I went to look up the rules governing the game. Alas, I was slightly disappointed. The official snooker specification is that the cushion height must be 0.635 plus or minus 0.010 times the ball's diameter. Almost right, but not quite. I was puzzled, so I asked snooker and pool dynamics expert David Alciatore why it is 0.635 and not 0.7. His answer injected a little reality into the issue. It seems the height is slightly smaller than the sweet spot height of 0.7 times the ball diameter so as to reduce the downward push of the rebounding ball onto the surface of the table near the cushion (called the gutter) and reduce wear on the table surface.
Did you manage to answer the puzzle posed in Outer space: On a clear day? If not, you can find the answer here.