
Outer space: Two's company, three's a crowd
Two people who get on well together can often find their relationship destabilised by the arrival of a third into their orbit. This is even more noticeable when gravity is the force of attraction involved. Newton taught us that two masses can remain in stable orbit around their centre of mass under their mutual gravitational forces - as do the Earth and the Moon. But if a third body of similar mass is introduced into the system then something quite dramatic generally happens. One body finds itself kicked out of the system by the gravitational forces, while the two that remain are drawn into a more tightly bound stable orbit.
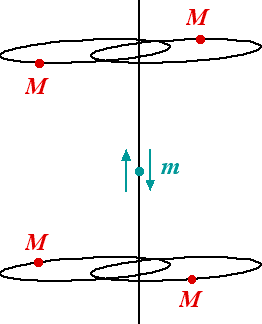
Jeff Xia's 5 body set-up
How does this happen? The little oscillating particle runs back and forth between the binary pairs, each time creating a little 3-body problem, it gets ejected and the binary recoils outwards to conserve momentum. The little particle then travels across to the other binary and the same scenario is repeated. This continues happening time and time again, without end, and accelerates the binary pairs so hard that they become infinitely separated in a finite time, undergoing an infinite number of oscillations in the process.
This example solves an old problem posed by philosophers as to whether it is possible to perform an infinite number of actions in a finite time. Clearly, in a Newtonian world where there is no speed limit, it is. Unfortunately (or perhaps fortunately), this behaviour is not possible when relativity is taken into account. No information can be transmitted faster than the speed of light and gravitational forces cannot become arbitrarily strong in Einstein's theory of motion and gravitation. Nor can masses get arbitrarily close to each other and recoil. When two objects of mass M get closer than a distance 4GM/c2 , where G is Newton's gravitation constant and c is the speed of light, then a "horizon" surface of no-return forms around them and they form a black hole.
The slingshot effect of gravity in the presence of gravity can be demonstrated in your back garden with a simple experiment. It shows how three bodies can combine to create a big recoil as they try to conserve momentum when they pass close to each other (in the case of astronomical bodies) or collide (as in our case).
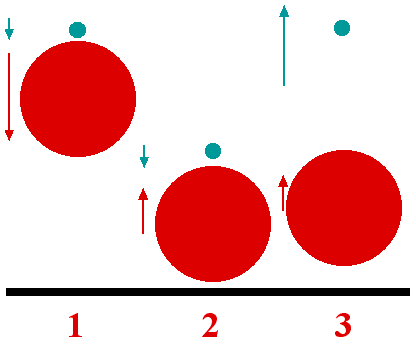
Don't try this indoors!
The three bodies will be the Earth, a large ball (like a basket ball or smooth-surfaced football) and a small ball (like a ping-pong or tennis ball). Hold the small ball just above the large ball at about chest height and let them both fall to the ground together. The big ball will hit the ground first and rebound, hitting the small ball on the way up while it is still falling. The result is rather dramatic. Can you show that the small ball bounces up to a height about nine times higher than it would have gone if it had just been dropped on the ground from the same height?
You might not want to do this indoors!
Did you manage to answer the puzzle posed in Outer space: A sense of proportion? If not, you can find the answer here!