Parabolati

Two shapes are similar if they're exactly they are the same shape, but a different size and/or located in a different position in space through rotation, translation or reflection. The amount by which one shape needs to be blown up (or reduced) to get the other is called the scaling factor.

Shapes of the same colour are similar.

All circles are similar, all squares are similar, and all equilateral triangles are similar too. But what about less simple shapes, such as parabolae? Let's see.

Are all parabolae similar?

First, some experimenting. The equations $$y=x^2$$ and $$ y=\frac{x^2}{1000}$$ both define a parabola. At first the two parabolae look very different. In the plot below the black curve is the former parabola and the blue curve (which looks like it coincides with the $x$-axis) the latter.

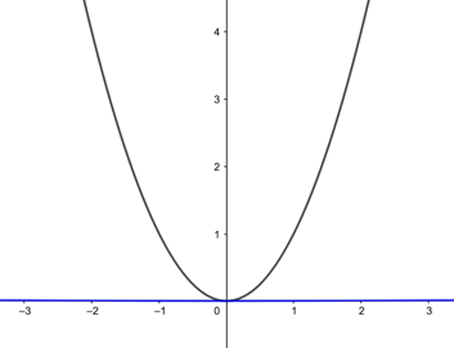
The black curve represents y=x² and the blue curve (which looks like it coincides with the x-axis) represents y=x²/1000.

However, when we zoom out so that we can see $x = 2000$, then the graph of $$y=\frac{x^2}{1000}$$ has a similar shape to the graph of $$y = x^2$$ in the first picture.

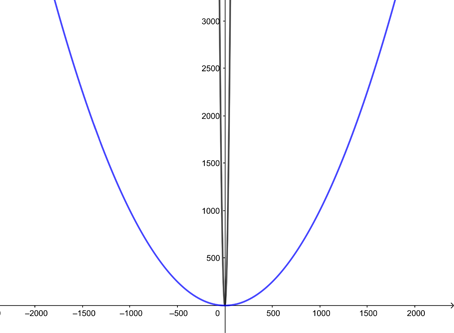
When you zoom out the graph of y=x²/1000 looks similar to that of y=x² in the previous picture.

Therefore, there is at least the possibility that all parabolae are similar.

The general case

Let's now look at the general case. A parabola can be defined as the graph of a quadratic expression, but it can also be defined as the set of all points that lie at the same distance to a given line (the directrix) and a given point (the focus) which is not on the line. You can always rotate a parabola, together with its focus and directrix, so that the directrix becomes a horizontal line and the opening of the parabola is pointing upwards. The rotated parabola is similar to the original one.

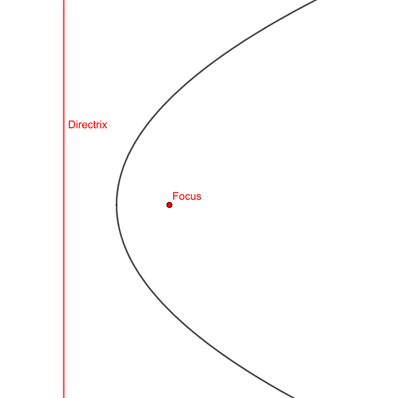
Generally, a parabola is the set of points that are at an equal distance to a given line and a point not on the line.

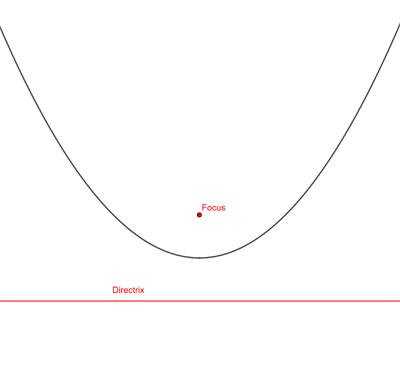
Rotating the parabola above through 90 degrees anti-clockwise gives a parabola whose directrix is horizontal.

Now we can impose a Cartesian coordinate system on the plane with the parabola sitting within it. We will do this in such a way that the point $(0,0)$ coincides with the vertex of the parabola. By the definition of a parabola, the vertex is the same distance away from the focus and the directrix. We'll call that distance $d$. The focus has coordinates $(0,d)$ and the directrix is given by the equation $y=-d.$

A parabola sitting in a coordinate system. We haven't labelled the axes as this works for any parabola.

We will now work out the formula that describes our parabola within the coordinate system. The distance between a point $(x,y)$ on the parabola and the focus is $$\sqrt{x^2+(y-d)^2},$$ by Pythagoras' theorem (see the diagram below). The distance between the same point and the directrix is $$y+d.$$

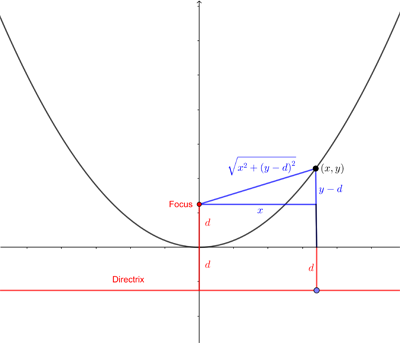
The distances from a point on the parabola to the focus and directrix.

By the definition of the parabola these two distances are equal so $$\sqrt{x^2+(y-d)^2} = y+d,$$ which means that $$x^2+(y-d)^2 = (y+d)^2.$$ Solving for $y$ gives $$y=\frac{x^2}{4d}$$ This is the equation for our parabola, which we will call $P.$

We will now see if this parabola is similar to the one given by the equation $$y=x^2,$$ which we call $Q.$ One way of achieving scaling in our coordinate system is to multiply each coordinate of a point within a shape by the same number. Let's take a point $(x,y)$ on the second parabola $Q$. Multiplying each coordinate by $4d$ gives the point $(4dx,4dy).$ Since $(x,y)$ lies on $Q$ we have $$y=x^2.$$ Multiplying both sides by $4d$ gives $$4dy=4dx^2=\frac{(4dx)^2}{4d}.$$ But this means that the point $(4dx,4dy)$ satisfies the equation of parabola $P.$ Thus multiplying the coordinates of each point on $Q$ by $4d$ gives a point on parabola $P.$ You can check that the converse is also true: dividing the coordinates of each point on $P$ by $4d$ gives a point on $Q.$ Thus, $P$ and $Q$ are similar: one is a scaled version of he other. This arguments works for whichever parabola we start with, showing that every parabola is similar to the parabola $Q$ given by $$y=x^2.$$ You can prove for yourself that this implies that all parabolae are similar to each other.

Other shapes

A parabola is an example of a conic section: a shape you get when you slice a cone with a plane. The other conic sections are the hyperbola, the ellipse, and the circle (which is in fact a special case of an ellipse).

The conic sections. Top row: a circle and an ellipse. Bottom row: a hyperbola (which also contains another curve not shown here) and a parabola. See here for more details on the conic sections.

It turns out that all hyperbolae with the same eccentricity are similar to each other, and that all ellipses with the same eccentricity are also similar.

You can also try your hand at other types of functions, for example exponential functions of the form $$y=q^x,$$ where $q$ is a positive real number. Are the graphs of exponential functions similar? We will leave that up to you to explore.

About the author

Forest Ho-Chen is a student (class of 2022) at George School in Newtown, Pennsylvania in the United States. He enjoys learning and writing about STEM and arts, and even created a journal for these subjects called MATES. At George School, Forest is a leader of the Math and Beyond Club, a captain of the Varsity Math Team, a manager of the Boys Varsity Soccer team, a cellist and conductor of the String Ensemble, and a writer and editor for the school newspaper, Curious George.