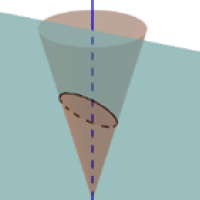
What do the circle, the ellipse, the parabola and the hyperbola have in common? They are all shapes you get when you slice through a cone. You get a circle when you intersect a cone and a plane that is perpendicular to the cone's axis. When you tilt the plane slightly the circle turns into an ellipse. As you tilt the plane further, it will eventually become parallel to one of the generating lines of the cone — that's a straight line lying on the cone and emanating from the apex. When this happens the intersection is a parabola. When you tilt the plane even further the intersection becomes a hyperbola. If you introduce a second cone so that the two cones touch at their apexes and have the same axis, then the hyperbola actually intersects both parts of this double cone. It's in terms of a double cone that the conic sections are usually defined, which is why we learn that the hyperbola has two disconnected parts (you can find out more about the hyperbola here.)
To see this in action, use the slider in the applet below to incline the plane.
Eccentric conic sections
There is also another way of defining the conic sections, which at first sight appears very different from what we just looked at. Forget about the third dimension for a moment and think of a plane with a line and a point in it. We will call the line the
directrix and the point, which is not on the line, a
focus. Now think of the shape $S$ made by all the points for which the ratio between the distance to the focus and the distance to the directrix is some constant $r$. That constant is called the
eccentricity of $S.$
It turns out that if $0
1$ then $S$ is an ellipse, if $r=1$ then $S$ is a parabola and if $r>1$ then $S$ is a hyperbola. You can explore this in the applet below. First use the blue slider to arrange the initial set-up: it varies the distance between the directrix and the focus. Then use the black slider to choose the eccentricity $r$. This also illustrates that there are whole families of ellipses, parabolas and hyperbolas: for each value of $f$ you get ellipses for all values of $r1$, a parabola for $r=1,$ and hyperbolas for $r>1.$
The ellipse you get for values of $ r 1$ is a symmetric object. By reflecting it in its vertical symmetry axis we get another focus point and a second directrix (both shown in the applet). By symmetry the ratio between the distance to the second directrix and the second focus is also equal to $r.$ As we increase $r$ towards $1,$ the second focus point moves further out to the right. When $r=1,$ and $S$ is a parabola, it has "disappeared to infinity". Then, as we increase $r$ beyond $1,$ the focus point and the second directrix appear from the left and together define the second arm of the hyperbola.
The eccentricity can be thought of as a measure of how far a conic section is away from being a circle. You can see in the applet above that
as the value of $r$ gets closer to $0$, the corresponding ellipse gets rounder and rounder. (At $r=0$ the conic section reduces to a point, but this doesn't mean that a shape of eccentricity $0$ doesn't exist — it's actually a circle! You will find out more below.) As the value of $r$ gets larger, the corresponding shape gets flatter; further away from being round.
Connecting the definitions
How are the two definitions of the conic sections connected? To find out, let's go back to the double cone. It turns out that you can find either one or two spheres that are tangent to (they just touch) both the double cone and the plane $P$ that defines the conic sections. These are called Dandelin spheres after the Belgian mathematician Germinal Pierre Dandelin who discovered them in 1822.
Use the slider below to incline the plane $P$ (in turquoise) and see the corresponding conic sections and red Dandelin spheres. You get a parabola for the value $t=3.$ (See below for an explanation of the other objects appearing in this applet.)
In the case of the ellipse there are two Dandelin spheres, both tangent to the same part of the double cone, in the case of the parabola there is only one, and in the case of the hyperbola there are two again, but this time each is tangent to a different part of the double cone. In the case of the ellipse and the hyperbola the plane $P$ that slices the double cone touches the Dandelin spheres in two points. These are exactly the focus points we used for the definition of the conic sections above. The two Dandelin spheres intersect the cone in two circles, which define two planes, shown in green. These planes intersect $P$ in straight lines — and these are exactly the directrix lines we used in our definition above. In the case of the parabola there is only one Dandelin sphere, which touches the plane $P$ in the point that is the single focus of the ellipse. The intersection of the corresponding green plane with $P$ defines the single directrix.
The circle is a special case. It arises when the slicing plane $P$ is horizontal and the two Dandelin spheres meet $P$ at the same point. This means that the two foci coincide. The plane $P$ is now parallel to the two green planes, so it can't intersect them. This means that there are no directrix lines; to put it differently, the directrix lines are "out at infinity" and therefore infinitely far away from the focus. The eccentricity of the circle — the ratio between the distance of points on the circle and the focus point to their distance to the directrix — can therefore be thought of as being equal to $0.$
But why doesn't the circle appear in applet 2 above? Instead, the conic section in that applet reduces to a point for $r=0.$ The answer is that in applet 2 we vary the eccentricity $r$ for a fixed value of the distance $f$ between the focus and directrix. By contrast, in applet 3 that distance changes as we change the inclination of the slicing plane $P.$ To keep $f$ constant in applet 3 as we incline the slicing plane towards the horizontal (so the conic section approaches a circle), we would need to also move the plane up the cone at a rate which has $P$ reaching the horizontal position exactly when its intersection with the cone consists of the apex only. Observing the conic section change on the plane $P$ as we do so would give us exactly the picture we see in the second applet: as the ellipse becomes rounder and rounder it also becomes smaller and smaller — at the point where complete roundness (eccentricity $r=0$) would be reached, the conic section reduces to a single point.
It turns out that the value of the eccentricity $r$ of the conic sections is given by two angles in this picture, which are best understood by taking a side-on view. The angle $\alpha$ is the one defining the steepness of the cone — for a cone with a vertical axis it's the angle between the horizontal and a generating line of the cone. The angle $\beta$ is the angle between the horizontal and the plane slicing the cone. It turns out that the eccentricity of the conic section corresponding to a given inclination $\alpha$ of the slicing plane is $$r=\frac{\sin{\beta}}{\sin{\alpha}}.$$
This tells you immediately that the eccentricity of the circle is $0$: the circle arises when the slicing plane is parallel to the horizontal, so $\beta=0.$ When the slicing plane is parallel to a generating line of the cone, we have $\alpha = \beta,$ so $r=1$ — that's the case of the parabola. As the slicing plane is inclined further, so we get a hyperbola, $\beta$ becomes bigger than $\alpha$ and tends towards $90^\circ,$ which implies that $r>1.$ Drag the point $A$ in the applet below to change the inclination of the slicing plane.
People have known about the conic sections since the ancient Greeks. Not only are they staples in geometry, they also find practical applications in the modern world (see Conic section hide and seek). The reason we like them most, though, is that the geometry behind them is beautiful!
About the author
Marianne Freiberger is Editor of Plus.